信息熵的理解

发表于 
记录一下看书收获。

1. 什么是熵

让我们先看一下维基百科对玻尔兹曼熵的来源描述和定义：

熵（Entropy），是一种测量在动力学方面不能做功的能量总数，熵的量度正是能量退化的指标。
熵亦被用于计算一个系统中的失序现象，也就是计算该系统混乱的程度。
1877年，玻尔兹曼发现单一系统中的熵跟构成热力学性质的微观状态数量相关。玻尔兹曼并假设：
S=k*lnΩ
公式中的k是玻尔兹曼常数，Ω则为该宏观状态中所包含之微观状态数量。这个被称为玻尔兹曼原理的假定是统计力学的基础。
统计力学则以构成部分的统计行为来描述热力学系统.

这就是玻尔兹曼的Entropy的来源了，而当普朗克来中国讲学时用到entropy这个词时，还没有对应名称，胡刚复教授偷懒地根据公式（dS=dQ/T），把“商”字加火旁来意译“entropy”这个字，创造了“熵”字（胡刚复与叶企孙同样是我国近代物理奠基人）。
不过上面是物理学衍生的玻尔兹曼熵，在1948年，克劳德·艾尔伍德·香农将热力学的熵引入到信息论，定义了信息熵的概念，因此它又被称为香农熵。

在信息论中，熵是接收的每条消息中包含的信息的平均量，又被称为信息熵、信源熵、平均自信息量。
这里，“消息”代表来自分布或数据流中的事件、样本或特征。

这即是熵的定义了，这里隐含的想法是，比较不可能发生的事情，当它发生了，意味着更多的信息。
所以熵也可理解为不确定性的量度[Measure of Uncertainty]，即越随机的信源的熵越大。

从玻尔兹曼熵到信息熵，后者是前者泛化(下文熵的表示)，那么Shannon当初是受玻尔兹曼的启发吗？
应该很难考证，毕竟不像欧拉一样会留下思考过程的手稿，不过有个故事或许可以说明：

“My greatest concern was what to call it. I thought of calling it ‘information’, 
but the word was overly used, so I decided to call it ‘uncertainty’. When 
I discussed it with John von Neumann, he had a better idea. Von Neumann 
told me, ‘You should call it entropy, for two reasons: In the first place 
your uncertainty function has been used in statistical mechanics under 
that name, so it already has a name. In the second place, and more 
important, nobody knows what entropy really is, so in a debate you will 
always have the advantage.”

上面是香农自述纠结于命名，而正是冯・诺伊曼考虑到类似统计力学，建议命名“熵(entropy)”，而且辩论中香农还有解释权的优势。如果理解不透也不必烦恼，因为香农还不认同《控制论》作者维纳对信息熵的定义呢，所以我们按照Shannon的理解。

2. 熵的表示

熵的表示是
$$ H(X) = E[I(X)] = E[-\ln(P(X))]$$
其中，P为X的概率质量函数（probability mass function），E为期望函数，而I(X)是X的信息量（又称为自信息）。I(X)本身是个随机变数。
当取自有限的样本时，熵的公式可以表示为：
$$ H(X) = - \sum_{i=1}^{m} p(x_i) \cdot \log p(x_i) $$
当p(x_i) = 1/m 是不是非常像玻尔兹曼的假设？不过玻尔兹曼其实是一个定义，而在Shannon，不禁会问，这个式子是怎么来的？

3. 信息熵的来源

知乎上为什么信息熵要定义成-Σp*log(p)，最高赞给出了答案，“假设两个随机变量x和y是相互独立的，那么分别观测两个变量得到的信息量应该和同时观测两个变量的信息量是相同的，即h(x+y)=h(x)+h(y)”, 然后通过这个特性使用柯西函数方程就可以推出Σp*log(p)的定义。

柯西函数方程是以下的函数方程：
    f(x+y)=f(x)+f(y)
此方程的解被称为加性函数。在有理数的范围中，可以用简单的代数得到唯一一类的解，
表示为f(x)=cx ，其中c任意给定的有理数。在实数中，这个方程仍然有这一类解。

知乎的答案几乎是正确的，但是有错。
这里其实都没有提及对h(x+y) 的约束，比如：x+y其实也是一个函数，“+”代表什么操作或者有什么约束？对于一个代数系统不定义该操作是难理解的，在这里是概率，也就是分别发生x／y事件[的概率]和同时发生事件x／y事件[的概率]带来的信息量是相同的。
换句话说，x+y 我们通常认为这是一个“加性”的操作，这样，我们得到的答案只能是类似f(x)=cx 的形式，而不是高赞答案里的Σp*log(p)。
事实上，看Bishop的《Pattern Recognition and Machine Learning》里，原文用的是H(x,y)而不是H(x+y).

3.1 信息量

让我们先定义一个函数 I, 他是事件概率为p(i)的事件i的信息量的度量(in terms of an event i with probability pi), 记作I(p), 并有如下属性(可参见Entropy_information_theory))：

a)  I(p)随p递增而递减
b)  I(p) ≥ 0
c)  I(1) = 0
d)  I(p1*p2) = I(p1) + I(p2), 即事件独立，具备可加性

令I 二次可导:

$$ I(p_1p_2) = I(p_1)+I(p_2) $$

$$ p_2I’(p_1p_2) = I’(p_1) $$

$$ I’(p_1p_2)+p_1p_2I’’(p_1p_2) = 0 $$

$$ I’(u)+uI’’(u) = 0 $$

$$ (u\mapsto uI’(u))’ = 0 $$

这里其实是用的是f’(x) = 0的特性推出f(x)=C 从而得出$I(u)=k\log u $ 对于$k\in \mathbb {R} $
实际上根据高等数学里，柯西函数方程 f(x+y) = f(x) + f(y) 这个函数方程的解是 f(x) = f(1) * x [假设f 是连续函数],为了转化为上面那个形式，令g(x)=f(e^x)就有
$$ g(x+y)=f(e^{x+y})=f(e^xe^y)=f(e^x)+f(e^y)=g(x)+g(y).$$

f(xy)=f(x)+f(y)特性见：Overview of basic facts about Cauchy functional equation
上述得到 事件p(i)的信息量计算公式，这就是数学的魅力。不过美中不足是信息量的单位是什么？对数学而言，人为的定义，当对数以2为底，单位是比特（bit），对数以e为底，单位是纳特/nats。
假设每个字母出现概率均等，英语26个字母，每个字母信息量是 I=-log(1/26)=4.7, 常用汉字2500，则信息量为11.3，这大约可以解释为什么表达同一个意思，汉字数量一般小于英文的 *字母 数量。

3.2 信息熵

有了信息量，我们就可以定义 随机变量X的平均信息量（期望信息量），也就是熵：
如果有一个系统S内存在多个事件S = {x1,…,xn}，每个事件的概率分布P = {p1, …, pn}，则整个系统的平均消息量,即熵为：

$$ H(X) = - \sum {p({x_i})} \log (p({x_i})) ~~~~ (i = 1,2, \ldots ,n)$$

4 熵的特性

4.1 定义

两点分布的熵
在上面熵的定义中，我们假设 两点分布的情况，假设p(x=1)=q, 代入即可得
$${\rm{H(X) = }} - \sum_{x \in X} {p(x)} \ln (p(x)) = - q\ln q - (1 - q)\ln (1 - q)$$

可以通过求导得出 q=1/2，即分布均匀时候，系统熵最大为ln2，而退化为确定性分布分布时最小为0，
那么这是不是意味着当分布均匀时候系统熵最大？确实如此，当满足已知条件的前提下，最大熵原理指出均匀分布熵最大，下文会证明。让我们来先熟悉几个定义：
联合熵 Jiont entropy
对于两个随机变量X，Y，X的取值为x1,x2…,xm,Y的取值为 y1,y2,…yn，令其联合分布p(x,y), 则其联合熵定义为：
$$ H(X,Y) = - \sum_{x \in X,y \in Y} {p(x,y)} \ln (p(x,y)) = - E(\log p(x,y)).$$
条件熵 Conditional entropy
同上述两个随机变量X，Y，则在X 已知的条件下Y的条件熵记做 H(Y|X) :

\begin{equation}\begin{split} H(Y|X) &=\sum_{x \in X} {p(x)H(Y|X = x)} \\
&=-\sum_x {p(x)} \sum_y {p(y|x)\log p(y|x)} \\
&=-\sum_x {\sum_y {p(x,y)\log p(y|x)} }
\end{split}\end{equation}
因某，式中x,y表示：$ x\in X,y \in Y$
相对熵 Relative entropy
相对熵，也被叫做KL距离，也即Kullback-Leibler散度（Kullback-Leibler Divergence），信息散度（information divergence），信息增益（information gain）。它主要用于衡量相同事件空间里的两个概率分布的差异。
典型情况下，对D(P||Q)P表示数据的真实分布，Q表示数据的理论分布，模型分布，或P的近似分布
同上述两个随机变量X，Y。假设p(x),p(y)是随机变量中取不同值时的两个概率分布，那么相对熵是：

$$ D({p||q}) = \sum_x {p(x) \log \frac {p(x)}{q(x)}} = E_p(x) \log \frac {p(x)}{q(x)} $$
互信息 Mutual Information
互信息,或转移信息（transinformation）是变量间相互依赖性(如相交信息量)的量度。
同上述两个随机变量X，Y，它们的联合概率密度函数为p(x,y)，其边缘概率密度函数分别为p(x),p(y)，则互信息I(x,y)定义：
\begin{equation}\begin{split}
I(X,Y) &= \sum_x \sum_y p(x,y) \log \frac{p(x,y)}{p(x)p(y)} \\
&= D(p(x,y)||(p(x)p(y))) \\
&= E_p(x,y) \log \frac {p(X,Y)} {p(X)p(Y)}
\end{split}\end{equation}
如维基百科介绍 直观地说，如果把熵 H(Y) 看作一个随机变量不确定度的量度，那么 H(Y|X) 就是 X 没有涉及到的 Y 的部分的不确定度的量度。这就是“在 X 已知之后 Y 的剩余不确定度的量”，于是第一个等式的右边就可以读作“Y的不确定度，减去在 X 已知之后 Y 的剩余不确定度的量”，此式等价于“移除知道 X 后 Y 的不确定度的量”。这证实了互信息的直观意义为知道其中一个变量提供的另一个的信息量（即不确定度的减少量）。
上面也可以看到，互信息也可以表示为两个随机变量的边缘分布 X 和 Y 的乘积 p(x) × p(y) 相对于随机变量的联合熵 p(x,y) 的相对熵。并且可理解为相对熵 X 的单变量分布 p(x) 相对于给定 Y 时 X 的条件分布 p(x|y) ：分布 p(x|y) 和 p(x) 之间的平均差异越大，信息增益越大(下文涉及)。

4.2 关系

  1. H(X,Y)=H(X)+H(Y|X)（链式法则）
    即：随机变量X,Y的联合熵等于其中一个随机变量的熵加上另一个随机变量的条件熵。其证明见如下：
    \begin{equation}\begin{split}
    H(X,Y) &= - \sum_x \sum_y {p(x,y)\log p(x,y)} \\
    &= - \sum_x \sum_y {p(x,y)\log p(x)p(y|x)}\\
    &= - \sum_x \sum_y {p(x,y)\log p(x)} - \sum_x \sum_y p(x,y)\log p(y|x)\\
    &= - \sum_x {p(x)\log p(x)} - \sum_x \sum_y p(x,y)\log p(y|x) \\
    &= H(X) + H(Y|X)
    \end{split}\end{equation}
  2. I(X,Y) = I(Y,X) ,这通过上述定义表达式对称性，可见。
  3. I(X,Y) = H(X) -H(Y|X) = H(Y) - H(X|Y), 如下证明：
    \begin{equation}\begin{split}
    I(X;Y) &= \sum_{x \in X,y \in Y} p(x,y) \log \frac{p(x,y)}{p(x)p(y)}\\
    &= \sum p(x,y) \log \frac{p(x|y)}{p(x)} \\
    &= - \sum_x \sum_y p(x,y)\log p(x) + \sum_x \sum_y p(x,y)\log p(x|y) \\
    & = - \sum_x p(x)\log p(x) - ( - \sum_x \sum_y p(x,y)\log p(x|y) )\\
    &= H(X) - H(X|Y)
    \end{split}\end{equation}
  4. D(P||Q) >=0 即：The relative entropy is non-negative
    证明需要用到吉布斯不等式，具体见wikipedia关于这个重要的不等式的意义证明。
    若$\sum_1^n p_i =1$ 及 $\sum_1^n q_i = 1$，且$p_i,q_i \in (0,1]$，则有：$ -\sum_1^n p_i \log p_i\leq -\sum_1^n p_i\log q_i $，等号成立当且仅当 $p_i=q_i \forall i$
    则，上述吉布斯不等式等价于：
    $$0\geq \sum_1^np_i\log q_i-\sum_1^n p_i\log p_i=\sum_1^np_i\log(q_i/p_i)=-D(P||Q)$$
    得证。
  5. I(X,Y) = H(X) -H(Y|X)=H(X)-(H(X,Y)−H(Y)) = H(X)+H(Y)-H(X,Y)
  6. I(X,Y) >= 0;见上面I(X,Y)的相对熵表示，同理推出I(X,Y),即The mutual information is positive
  7. 也可证 H(X,Y) ≤ H(X)+H(Y), 其实这条可推广至多个变量，即Less than or equal to the sum of individual entropies
  8. H(X,Y) ≥ 0, H(X)≥0 joint entropy非负性
  9. H(X|Y ) ≤ H(X).Additional information never increases entropy，由3可证，也可根据计算式得证，且仅独立于X,可等。
  10. H(X,Y,Z) = H(X) + H(Y|X) + H(Z|XY) ≤ H(X) + H(Y) + H(Z)
  11. H(X,Y)≥ max[H(X),H(Y)]，即Greater than individual entropies
  12. 还有许多特性，不一一列举。在《通信的数学原理》中香农列举许多特性，并得到许多有趣推论。
    最后，引用wikipedia一张图来帮助记忆这几种熵,或参考Joint entropy, Conditional_entropy。
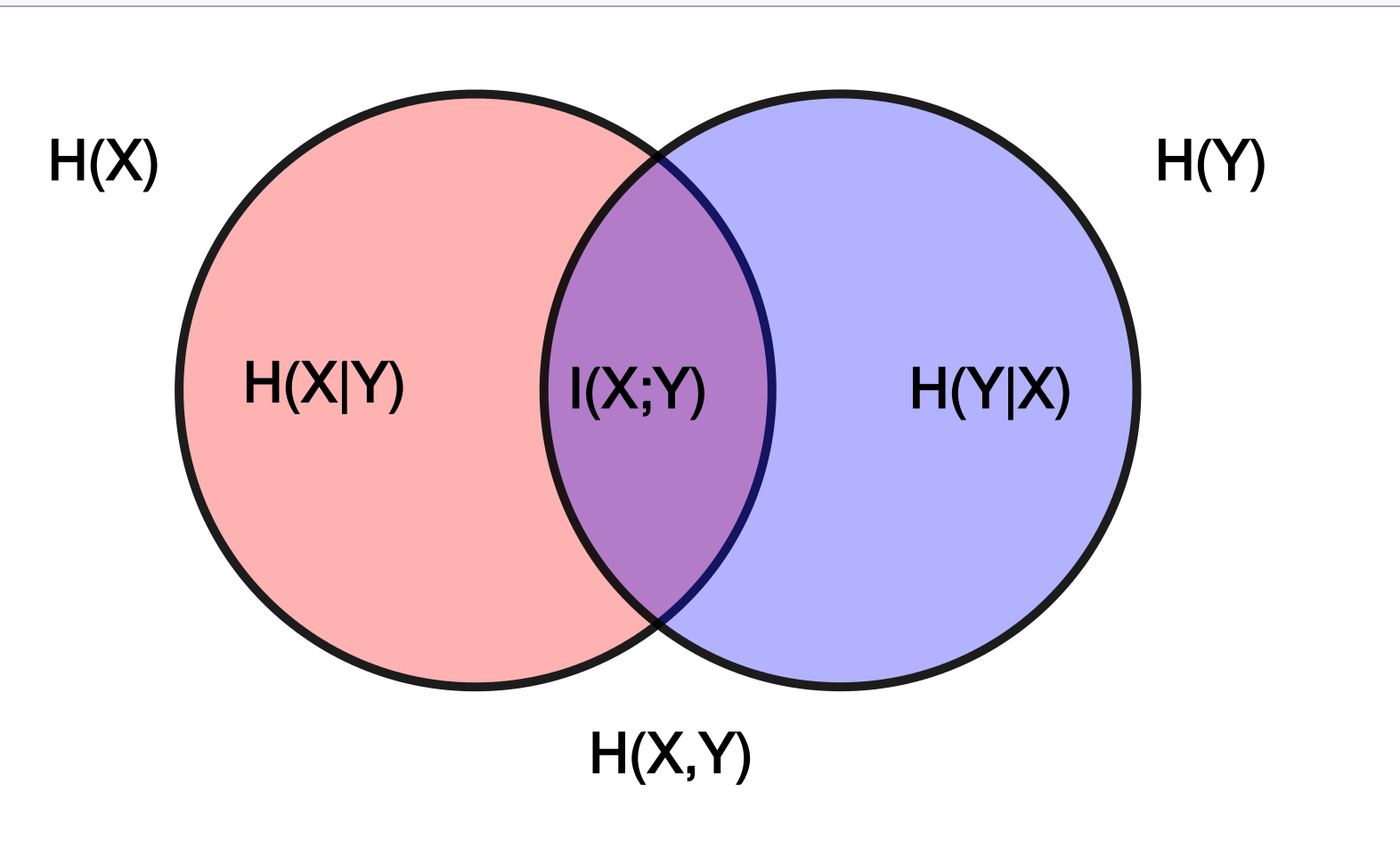
    Venn diagram for various information measures associated with correlated variables X and Y.

4.3 可加性 - 更好的理解信息熵

  1. 怎么去理解可加性？怎么理解 H(X,Y)=H(X)+H(Y|X)链式法则？
    其实香农在最初的著作里，用图形象的表达出来了，有助加深理解
    Shannon-entropy_ex
    信息熵的计算不依赖事件先后顺序，也即，假设三个事件P，有p1=1/2,p2=1/3,p3=1/6，我们既可以认为三个时间同时发生，如上图左，也可以是首先有两个事件p1=p2=1/2，然后在第二事件又分为p1=2/3,p2=1/3，所以信息熵H(1/2,1/3,1/6)=H(1/2,1/2)+1/2*H(2/3,1/3)。
    一个推导
  2. 《数学之美》里，吴军也曾分别举了猜球队冠军、骰子猜概率、王小波的例子形象化信息熵。
  3. 有个说法是思考如下问题：假设一共有N个球，扔到k个桶中。但这些桶大小是不同的。假设扔到第i个桶里的概率是pi，即第i个桶里有ni个球，那么一共有多少种不同分法（状态数）？
    得到结果后将其联想到玻尔兹曼的熵模型。（这个问题的解法其实可以关联到欧拉创造的神奇的伽马函数，这里不展开了）。

  4. 为什么要创造信息熵这个概念？其实对应物理／数学模型最大熵的概念

    The principle of maximum entropy states that, subject to precisely stated prior data
    (such as a proposition that expresses testable information), the probability distribution
    which best represents the current state of knowledge is the one with largest entropy.
    Another way of stating this: Take a precisely stated prior data or testable information
    about a probability distribution function. Consider the set of all trial probability distributions
    that would encode the prior data. Of those, one with maximal information entropy is the proper distribution, according to this principle
    这很符合人们在解决某系问题时通用的模式，即在已知部分事实的前提下，对未知分布最合理的推断就是符合已知事实的最不确定或最随机的推断。

  5. Shannon使用熵推导出压缩极限理论, 指出了无损压缩文件的极限，也导致一些有损压缩算法的诞生，比如google的WebP支持有损和无损压缩。
  6. 搜索引擎使用的文档相关性，TD-IDF算法，其实可以理解为相对熵的应用：词频在整个语料库的分布与词频在具体文档中分布之间的差异性。
  7. 对于孤立理想气体，在麦克斯韦-玻尔兹曼分布下是稳定态，各相均等，此时是最小熵产生状态。同样的，信息系统有最小鉴别信息原理的说法，可以参考大名鼎鼎的H定理，微观推导出热力学第二定律，也是信息熵公式的前身。
    事实上，玻尔兹曼公式的另一种等价表述形式正是 $S=-k \sum_1^n p_i \log p_i)$ ， 其中i标记所有可能的微观态，p(i)表示微观态i的出现几率.
    统计熵揭示一个孤立系统的倾向于增加混乱程度，但”宇宙是一个孤立系统“严格来说只是个未被验证的假设。还有H公式等，二者简直是太相似了，甚至通信数学原理许多推论，以及最大熵原理最小鉴别信息原理等都是如此相似？这里物理和信息论如此和谐，这是一种自然现象的两种形式吗，还是二者其实是基于同一数学模型所致？要揭开这样的问题可能需要正态分布／泊松分布／二项分布等各种分布即gama函数等现代概率统计学基础去解释了。
  8. 也有使用Shannon熵和热力学熵曲解释现代计算机在处理大量信息时，必须解决散热问题的，如Landauer法则。
  9. 玻尔兹曼熵处理的是根据运动的热力学分子均衡状态下，熵增。
    而香农观点来看，其实把我们看到的信息，比如一段文字，看成是气体分子，不同的是这里的“气体分子”是比玻尔兹曼的要规则，也即熵小一些。从数学角度去理解：熵就是系统各状态自信息量的数学期望
    信息熵或者说熵，或者不论是维纳还是香农的信息论，可以说，比如许多熵减的系统／过程都可以用熵解释，当然这么讲可能不是很有用。
  10. 最后，你想过信息论可以解释堆排序为何比快排慢吗？
    heapsort和quicksort排序耗时都是O(n*logn), 但为什么quicksort表现会更好？非常建议看看MacKay的Heapsort, Quicksort, and Entropy，【如果被墙，可以看这里】不同于常见的思考问题角度，这篇文章里作者神奇的使用了信息论来解释，每次比较，quicksort获得有用信息的概率比heapsort均等。信息论还可以解释排序极限为何是O(nlogn)
    不过这里应该用“阐释”比较好，公式化的论证见TAOCP。
    思考下：Java 7偏后版本引入了里面性能被证明更好的TimSort的快速排序(不要再认为是课本里说的二分快排了)，是不是也可以用信息论解释？（TimSort的争议）

5 最大熵模型

这一段简要介绍最大熵模型的由来。

5.1 交叉熵Cross entropy)

先看一下交叉熵的定义：
对随机事件p，假设其真实概率分布为p(i)，观测得到其概率分布为q(i)[即实验分布]，则定义交叉熵为：
$$H(p,q) = E_p[-\log q] = -\sum_1^m p(x_i) \log{q(x_i)} $$

如上，假设p代表一个样本的真实的信息分布，则其信息量为H(p)，q为模型预测分布，则用q来估计真实分布p的样本的信息量为H(p,q),则冗余信息量D(p#q)=H(p,q)−H(p)由下面运算发现即是KL散度
\begin{equation}\begin{split} H(p,q) &= -\sum_x p(x) \log q(x) \\
&= -\sum_x p(x) \log \frac{q(x)}{p(x)}p(x)\\
&= -\sum_x p(x) \log p(x) -\sum_x p(x) \log \frac{q(x)}{p(x)}\\
&= H(p)+ D(p||q)
\end{split}\end{equation}

很容易发现：$H(p,q)=H(p)+D_{KL}(p||q) $ ，即：相对熵=交叉熵-信息熵, 信息熵H(p)是可视作不变，因此交叉熵也即损失函数。
好了，介绍了这么多，那么你遇到过这样的问题吗：
设有离散随机变量 X，我们并不知道X的概率分布p(x)，但已知其与若干函数的期望满足如下:$ \sum_{x \in X} p(x)f_m(x)=C_m ,x \in X, m=1,2,…,M $，求p(x)最佳估计P̃ (x).
这可以追溯到过定／欠定问题，下面摘录李航的《统计学习方法》来描述：
对于分类问题，假设现有训练数据集 $T={(x1,y1),(x2,y2),….(xn,yn)}$
最大熵模型就是分别根据已有的输入X和输出Y集合去学习训练数据的条件概率分布P(y|x)，应用最大熵原理去学习分类能力最好的模型.
上面，我们定义(x,y)为 特征，(xn,yn)就是某特征的 样本
对于给定的训练数据集，我们可以确定联合分布P(X,Y)的经验分布P̃ (X,Y),以及边缘分布P(X)的经验分布P̃ (X)P~(X)，即:

$$ \tilde{P}(X=x,Y=y)=\frac{count(X=x,Y=y)}{N} $$
$$ \tilde{P}(X=x) = \frac{count(X=x)}{N}$$
其中count(⋅)表示满足条件在样本中的计数，N表示总的训练样本容量

现在引入 特征函数f(x,y)，它是描述输入x与输出y之间满足的某一事实，f(x,y)则定义为二值函数:
$$
f(n) = \begin{cases} 1, & \text{if x,y满足某一事实} \\
0, & \text{else} \\
\end{cases}
$$

对于任意的特征函数f(x,y)，令 $ E_{\tilde{P}}(f)$表示特征函数f在训练数据集T上
关于$ \tilde{P}(x,y)$的数学期望，也即 样本特征函数期望值有:

$$ E_{\tilde{P}}(f) = \sum_{ x,y} \tilde{P}(x,y) f(x,y) $$
另记$E_{P}(f)$表示特征函数f在训练数据集T上关于P(x,y)的数学期望，有:
$$ E_P(f) = \sum_{ x,y} {P(x,y) f(x,y)} $$

为了计算P(y|x)，根据Bayes我们可以做如下转换$ P(x,y) = P(y|x) \cdot p(x)$
, p(x)未知，但是我们此时可以使用$\tilde{P}(x)$进行近似,也就是最终有:
$$ E_P(f) = \sum_{x,y} P(y|x) \tilde{P}(x) f(x,y)$$
我的期望是：$E_{\tilde{P}}(f) = E_P(f)$,即：

$$\sum_{x,y} \tilde{P}(x,y) f(x,y) = \sum_{x,y} P(y|x) \tilde{P}(x) f(x,y)$$

上述式子就可以作为模型的约束条件，假如有n个特征函数，则就会有n个约束条件(实际中一般特征的维度就是约束条件的个数)
用C来表示满足约束的模型集合:

$$ C= {P|E_{\tilde{P}}(f) = E_{P}(f),I=1,2,3..n} $$

满足约束条件同时使用P(y|x)的熵最大的模型即为最大熵模型.
最后，为了获取条件概率的分布，还需要其相应的条件熵
$$H(P)= - \sum_{x,y} \tilde{P}(x) P(y|x) log P(y|x)$$

至此，最大熵模型的公式定义结束，再次总结一下，
给定数据集 $ {(x_i,y_i)}_1^N $，特征函数$f_i(x,y)，i= 1,2…,n$，根据经验分布得到满足约束集的模型集合 C, 公式化的描述：：

\begin{align}
\underset{P \in C}{max} &\quad H(P) = - \sum_{x,y} \tilde{P}(x) P(y|x) \text{log} P(y|x) \\
st. &\quad E_{P}(f) = E_{\tilde{P}}(f),I=1,2,3..n \\
&\quad \sum_y P(y|x)=1
\end{align}

至此为止，介绍了信息熵，基本的几种熵，熵的特性，以及最大熵的意义和定义。
对于最大熵，其求解方法，与似然函数关系等等还有许多可以介绍的，不过限于篇幅，需要另起一篇再探讨了。

参考：

  1. wikipedia
    History of entropy
    Entropy_(information_theory))
    熵 (信息论))
  2. 高等数学第六版 同济版
  3. 《统计学习方法》.李航著
  4. The Mathematical Theory of Communication. by Claude E.Shannon and Warren Weaver
  5. Toplanguage https://groups.google.com/forum/#!forum/pongba