正确理解一致性哈希

发表于

intro1：正确地理解一致性哈希
intro2: 介绍几种其他优质一致性哈希算法
intro3: Redis Sentinel和Cluster

之前写过几篇哈希函数的blog，本文继续对一致性哈希(Consistent Hashing，本文简称CoH)部分作进一步补充，讨论下CoH的作用，以及其他一致性哈希实现。
阅读本文前可先阅读下 Consistent Hashing: Algorithmic Tradeoffs，需FQ，原文概要介绍了Consistent Hashing、Jump Hash、Multi-Probe Consistent Hashing(MPCH)、Rendezvous Hashing、、Maglev Hashing等几种一致性哈希方式，本文主要从实用角度探讨下一致性哈希实现，同时讨论下不同于原文的几点思考。

什么是一致性哈希

需要先弄清楚这个“一致”是什么意思？即什么是一致性哈希？为什么需要一致性哈希？
wikpedia上CoH定义：
一致性哈希(consistent hashing) 是一种特殊的哈希算法。在使用一致哈希算法后，哈希表槽位数（大小）的改变平均只需要对 K/n 个关键字重新映射，其中K是关键字的数量，n是槽位数量。然而在传统的哈希表中，添加或删除一个槽位的几乎需要对所有关键字进行重新映射。
从上述定义你也可以看出把“consistent”(一贯的)翻译成一致性或许并不准确，因为这里 其实是想表达前后一贯的（即哈希槽分布尽量前后一致），和我们平常理解的CAP或者ACID里的consistency(一致性)其实完全不同，后者是全局的一致性，不侧重先后。或许翻译成稳定哈希/稳定散列更合适。

CoH由MIT的David Karger及其合作者在他们1997年发表的论文《Consistent Hashing and Random Trees: Distributed Caching Protocols for Relieving Hot Spots on the World Wide Web》中提出，并介绍了CoH在系统添加或删除节点只需要移动K/n项，从而减少大型Web应用中系统部分失效带来的负面影响（健壮缓存）。

上述，一致性哈希首先是可以解决分布式系统中怎么将数据（如一类关键值key集合）如何分散到所有分布式系统中的节点，并且可以有效地将消息转送到唯一一个拥有查询者提供的关键值的节点的算法，这在分布式系统概念里有个专门术语：分布式散列表（distributed hash table，简写 DHT），P2P、多播、DNS以及各种去中心化的分布式系统中都含有DHT的影子。像在P2P文件共享技术这条路上，就经历过集中式、多播、结构化网络(DHT)等阶段，将海量的keyspace通过足够防碰撞的哈希函数生成散列值(如128bit、160bit)，再分散到多个节点上，所以通常要求DHT要有：离散性(Autonomy and decentralization, 去中心化)、伸缩性(Scalability,成千上万个节点，依然高效）、容错性(Fault tolerance, 节点不断加入或离开，系统仍足够可靠)。P2P中的四大算法之一中的Chord，据说是莫里斯蠕虫和Y Combinator创建者莫里斯提出的，就是基于一致性哈希实现的。

一致性哈希的实现

一致性哈希算法可参考一致性哈希算法原理 这片文章，本文不详述, 简单来说，如维基描述：
一致哈希将每个对象映射到圆环边上的一个点，系统再将可用的节点映射到圆环的位置。查找某个对象对应的节点时，需要用一致哈希算法计算得到对象对应圆环边上位置，沿着圆环边上查找直到遇到某个节点，即为对象应该保存的位置。当删除一台节点时，该节点上的所有对象都要移动到下一节点。添加一节点到圆环边上时，这个点的下一节点需要将这个节点前对应的对象移动到新节点上。

相比早期DHT，一致性哈希带来了具平衡性(Balance)、单调性(Monotonicity)、分散性(Spread)、负载(Load)、平滑性(Smoothness)等诸多特点，这在Couchbase、OpenStack、Amazon的Dynamo、Cassandra、Akka的router、Azure Cosmos DB都有用到。
请注意Redis本身是没有用到一致性哈希的，只不过是Jedis这样的redis外围工具支持一致性哈希。像“描述下Redis的一致性哈希算法”或者“一致性哈希因为虚拟节点而做到分布均匀”这类不正确的观念并不少见，笔者甚至曾经见到过美团的专家也会用这种错误的问题去提问，有趣的事美团技术博客有篇文章讨论过为什么他们的KV不选择一致性哈希: 美团点评万亿级 KV 存储架构演进。
首先，Redis没有consistent hashing的概念，而Redis Cluster也未使用consistent hashing，而是用了hash slot的概念。
其次，虚拟节点不是为了提高映射结果的均匀性，正如之前文章提到的，如果哈希值对160(个节点)取模能够做到均匀，那么没有理由这个哈希值对4(个节点)取模就做不到均匀，真正提高均匀性的是一致性哈希时使用的哈希函数。比如jedis中的murmurhash，同样 Cassandra也是mumurhash(org.apache.cassandra.dht有详尽的代码)，其他C实现可能FNV哈希。
再其次，虚拟节点真正起到均衡作用是在出现节点变动时，当然这也和虚拟节点的分布有关。
最后其次，虚拟节点带来另外一个好处是可以支持权重，比如我们想实现三个节点A:B:C分别5:3:2的分布，那么我们按照这个权重生成虚拟节点就能做到。
这里不展开一致性哈希算法，不过我还是放张图便于理解：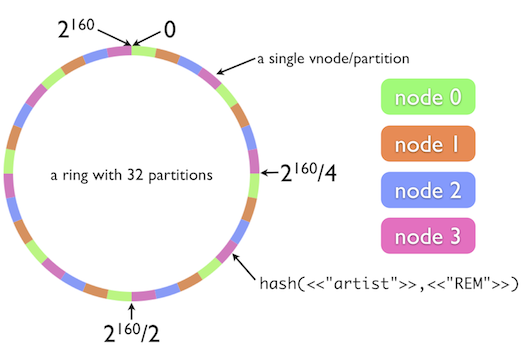

来源：https://dzone.com/articles/simple-magic-consistent

先不考虑虚拟节点，对于一致性哈希来说，要想做到 consistent即DHT的稳定性，假设圆环上有4个结点，扩容时我们想在圆环增加一个节点变成5节点集群，那么为了数据均衡，我们期望尽量有1/5的数据能迁移到新节点上，而删除节点时至少需要迁移走(该节点上的约)1/4的数据（请记住这个结论下文会用到）。
所以，一个需要避免的误区是，设计一致性哈希不是为了均衡，consistent hashing重点在于 consistent，前后一贯，也就是稳定性，即上述挂掉一个节点尽量不引起其他节点数据再次分布，而上述1/4的数据能否均衡分布到剩余的节点则是第二个特性了，虚拟节点可以一定程度做到，但还有改进的余地，比如下文要介绍的来自Google的Jump Hash。

一致性哈希虚拟节点按什么顺序分布

你有注意到在一致性哈希里虚拟节点怎么生成以及又是怎么分布的吗？比如下面ABC三节点的虚拟节点是按下图方式即ABC顺序交叉分布的吗？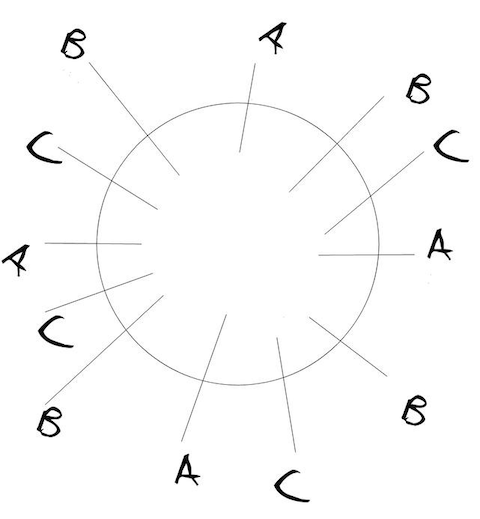

显然不是，否则假设删除物理节点B时，B节点上的数据永远落在物理节点C上了，这和不设虚拟节点效果一样了。
我们看CoH的wikipedia上附录里的各语言实现，实际上确实都不是。
如python实现：The Absolutely Simplest Consistent Hashing Example

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
def _hash(self, key):
    """Given a string key, return a hash value."""
    return long(md5.md5(key).hexdigest(), 16)
def _repl_iterator(self, nodename):
    """Given a node name, return an iterable of replica hashes."""
    return (self._hash("%s:%s" % (nodename, i))
            for i in xrange(self.replicas))
def __getitem__(self, key):
    """
    Return a node, given a key.
    The node replica with a hash value nearest
    but not less than that of the given
    name is returned.   If the hash of the
    given name is greater than the greatest
    hash, returns the lowest hashed node.
    """
    hash_ = self._hash(key)
    start = bisect.bisect(self._keys, hash_)
    if start == len(self._keys):
        start = 0
    return self._nodes[self._keys[start]]

上述replicas可认为是每个节点虚拟化的数量，_repl_iterator就是添加节点时调用的方法，上述代码可认为是添加虚拟节点就是对nodename和下标i做md5并将此作为key添加到一个bisect有序集合里，也就是虚拟节点是按md5有序而，md5随机性且无法反映出nodename+i的顺序性，也就是说虚拟节点不是ABC这样有序性交叉分布环上的。
Jedis的一致性哈希和上面附录里的Java代码类似：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
private void initialize(List<S> shards) {
  nodes = new TreeMap<Long, S>();
  for (int i = 0; i != shards.size(); ++i) {
    final S shardInfo = shards.get(i);
    if (shardInfo.getName() == null) for (int n = 0; n < 160 * shardInfo.getWeight(); n++) {
      nodes.put(this.algo.hash("SHARD-" + i + "-NODE-" + n), shardInfo);
    }
    else for (int n = 0; n < 160 * shardInfo.getWeight(); n++) {
      nodes.put(this.algo.hash(shardInfo.getName() + "*" + shardInfo.getWeight() + n), shardInfo);
    }
    resources.put(shardInfo, shardInfo.createResource());
  }
}
public S getShardInfo(byte[] key) {
  SortedMap<Long, S> tail = nodes.tailMap(algo.hash(key));
  if (tail.isEmpty()) {
    return nodes.get(nodes.firstKey());
  }
  return tail.get(tail.firstKey());
}

上述this.algo.hash默认是murmurhash，即，当使用默认权重1时，每节点对应160个虚拟节点，这些虚拟节点对应key做murmurhash结果作为key存入TreeMap，value就是shardInfo即物理节点信息。
通过key定位虚拟节点就是通过 getShardInfo 方法实现的，Java中TreeMap的tailMap方法返回NavigableSubMap，表示其键大于或等于fromKey的部分视图此时：

  • tail非空
    则直接返回第一个，即表示treemap中键值为该虚拟节点或者第一个大于该虚拟节点的虚拟节点。
  • tail为空
    即此时不存在大于等于该键值的虚拟节点，表示该节点处于环尾，显然此时返回该环第一个，即nodes.get(nodes.firstKey())

上述，正是因为随机打乱虚拟节点顺序，使得删除一个物理节点时，该节点上的数据能有机会均匀分布到其他物理节点，注意这里是分布到临近的其他节点的机会是均匀的，而非节点上的数据会均匀分布到其他物理节点，数据分布能否均匀要看当前的数据节点分布。
随机打乱虚拟节点顺序也侧面说明增加虚拟节点能使数据更加均衡这种说法是错误的，除非原始的输入数据本身就是不均衡的或者增加的虚拟节点不是随机的，得到的可能至多只是暂时均衡态。

一致性哈希时间复杂度

上述代码展示了定位虚拟节点/物理节点的方法，如Java的TreeMap，本身是一种二分查找，也就是说，一致性哈希时查找节点时间复杂度是O(logN)，这里的N指的是虚拟节点的数量，而非物理节点，同样的空间复杂度是O(N)。
这里也可以看到通过 Jedis 设置节点权重时候，最好不要用10:20:70这种方式，相比 1:2:7 浪费十倍内存，也增加查找时间。

Jump Consistent Hash

顾名思义，也是一种一致性哈希，Google 于2014年论文A Fast, Minimal Memory, Consistent Hash Algorithm提出的一种实现，简单到仅5行代码，性能极大优势，分布完全均衡的一致性哈希算法：
In 2014, Google released the paper “A Fast, Minimal Memory, Consistent Hash Algorithm” known as “Jump Hash”. The algorithm was actually included in the 2011 release of the Guava libraries and indicates it was ported from the C++ code base.
Jump Hash addresses the two disadvantages of ring hashes: it has no memory overhead and virtually perfect key distribution. (The standard deviation of buckets is 0.000000764%, giving a 99% confidence interval of 0.99999998 to1.00000002).

看到Jump Consistent hash，笔者觉得这个起名字有点数学里像随机游走或者马尔可夫过程的一个概念：醉汉漫步或者酒鬼漫步，数学家波利亚证明在一个二维平面上随机东西南北游走的酒鬼回到家的概率竟然是100%。这里jump就是类似随机函数可左可右，围绕某点跳来跳去，即便如此还能保证 consistent，即分布稳定，这个名字本身是不是也包含了一种幽默。

如上述，Guava提供的consistent即是jump consistent hash的实现，代码在Hashing#consistentHash(long input, int buckets)，其中的LinearCongruentialGenerator就是线性同余法(LCG)生成伪随机数。这里采用Google论文里的C代码稍微改动下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
// JumpConsistentHash
int JumpConsistentHash(long key, int num_buckets) {
    long b = -1, j = 0;
    while (j < num_buckets) {
        b = j;
        key = key * 2862933555777941757ULL + 1;
        j = (b + 1) * (double(1LL << 31) / double((key >> 33) + 1));
    }
    return b;
}
// ch函数，JumpConsistentHash的另一种易读表示
int ch(int key, int num_buckets) {
    random. seed(key) ;
    int b = -1; //  bucket number before the previous jump
    int j = 0; // bucket number before the current jump
    while(j<num_buckets){
        b=j;
        double r=random.next(); //  0<r<1.0
        j = floor( (b+1) /r);
    }
    return b;
}

可以看到代码不消耗内存存储，而且性能也是O(logN)，但理论上跳跃查询比二分查找快，原论文测试数据可以看到超一千节点时性能比CoH少一两个数量级了。
Jump consistent hash的设计理念非常简单，只关注需要移动的数据移动到新桶里。即假设当bucket数量从n到n+1变化时，需要把一些对象从旧桶移动到新桶，同时其它保持不变，为了达到均匀和不变两个效果，我们只要移动1/(n+1) 的数据。
原论文通过构造ch这个函数，一步步详细的的构造和论证ch是如何实现均匀效果的，但如何理解并设计ch函数呢？笔者认为理解第一步比较关键，之后基本数学可推导，看第一个函数：

1
2
3
4
5
6
7
8
9
int ch(int key, int num_buckets) {
    random.seed(key);
    int b = 0;
    for (int j = 1; j < num_buckets; j++) {
        if (random.next() < 1.0 / (j + 1))
            b = j;
    }
    return b;
}

这里其实两点考虑：
已知ch(key, n)表示将key分配桶，该结果就是桶编号(桶号0开始)。

  • 那么ch(key, n+1)有两种结果：ch(key, n)或者新增的桶号n，并且最好是n/n+1的概率为ch(key, n)，1/n+1概率为n
  • 需要设计一种函数，实现上述概率特性。

我们知道计算机里有个伪随机数(如LCG)的概念，只要初始种子确定(上述以key作seed)，那么随机序列就具有：确定和足够随机的两个特性，或者说 确定的随机性。
这种思路其实还是很惊艳的，数学天才拉马努金就经常构造出出人意料的数学公式而震惊世人，这些数学公式常人很难想到，但一旦看到就会觉得不可思议：大自然中的数原来还有这个规律。欧拉和高斯也是“猜”/“捏造”数学公式的高手。
上述for循环就是实现了当这个函数进行从n到n+1桶扩散时，有1/n+1的概率是b=n，即哈希到新桶里的。也意味着n/n+1的概率不变。
不过上述是O(n)时间的，作者进一步将ch函数变形了下，得到上文代码所述。这里有推导过程：jump consistent hash的逻辑详解
不过也可这样简单理解：
已知某次从i到i+1时不变的概率：$P(ch(key, i)==ch(key, i+1)) = i/(i+1)$，上一次随机序列得到的桶号是b，递归展开就得到多次不变的概率 $P(ch(key, b+1)==ch(key, i))$为 $(b+1)/i$，反之则是变的概率。

上述分析，可以看到，只要伪随机数足够随机，jump hash在桶新增/删就能足够均匀。另外，我们知道桶的变化依赖随机序列，也即仅当新桶位于末尾时才有意义，也就是说只能在尾部增删节点，这是Jump Consistent Hash不足之处。

Maglev一致性哈希

上述Jump Consistent Hash尾部增删节点不适合通常应用，Google在2016年发布的一篇论文中介绍了他们的网络负载均衡器使用的另外一种一致性哈希算法：Maglev，适合任意节点增删同时又兼具非常好的性能、consistent、均衡性，非常适合负载均衡的场景, 或许dubbo的ConsistentHashLoadBalance可以考虑下。
Maglev实现的思路就是查找表(lookup table)，类似二次哈希生成，借助两个哈希函数，为每个节点生成一个permutation偏好序列，填满lookup table。
笔者需要进一步阅读了解Maglev具体实现，所以不再具体讨论，附件列出几个参考链接。

题外话：Redis Cluster怎么实现DHT

一些Redis外围支持consistent hashing模式实现redis的DHT，如Jedis、Twemproxy。
Redis集群为什么不使用consistent hashing呢？
对于分布式集群机器故障是必然的事，所以容灾是必须的，通常副本数据就是常见的灾备方案，像redis sentinel模式和cluster模式都需要master-slave(master-replica )数据备份做HA/故障恢复。故障下线不是本文考虑重点，我们考虑下动态水平扩容/缩容。
事实上，在使用一致性哈希系统里，如果我们把每个节点的数据都写到他的邻居节点，那么增加/删除节点时我们总是可以从邻居节点读取，同时不需对DHT算法作较大改动，但事实上，至少笔者很少见到哪些分布式系统(如各种nosql/kvstore)是这么做的，我们思考一个场景：上述情况时删除/增加的节点后如果再次增加/删除时，之前迁移的数据是否需要或者如何还原到对应节点？同样的变动两个连续的节点又怎么办呢？可能会引入过多复杂性或者增加寻址的次数。Cassandra就曾有类似思想，但后来的Vnode/rack机制引入了node table概念，这和Redis Cluster的slot不谋而合，只不过Cassandra的容灾通过各个节点间相互备份数据实现，而Redis Cluster没有，目前似乎只能简单的做主从复制同步。

Redis Cluster之前Jedis Sentinel也是常用的操作Redis集群方法，其ShardedJedis就是一致性哈希， 所以Redis Sentinel模式其实是极不方便水平动态扩容 / 缩容的，相信每个使用纯Sentinel搭建Redis集群的开发/运维在扩容时都会遇到这个恼人的问题（所以会在访问量少的时候，运行程序遍历redis数据并计算重新hash到新节点），而Redis Cluster模式则引入了Slot概念，扩容时添加了节点后，只需要运行reshard命令即可通过运维人员就可以路由部分数据到新节点。
此外，Codis的Pre-sharding的技术也是采用类似slot概念实现数据分片，默认分为1024个slot，先对key进行crc32运算，所以codis可以水平动态扩容 / 缩容，而对于Sentinel，key分布信息完全是应用(如jedis哈希函数/虚拟节点数)决定的。
不知道读者是否发觉这里有趣的现象，一方面jedis sentinel 有一致性哈希似乎可用来处理Redis集群中节点的挂掉/增删，另一方面我们的Redis集群却常用主备来防止节点挂掉，多么矛盾。

其实笔者认为redis作者总结过的redis作为缓存时适用一致性哈希，作为存储时则选择Slot的观点很实用：

  • If Redis is used as a cache scaling up and down using consistent hashing is easy.
  • If Redis is used as a store, a fixed keys-to-nodes map is used, so the number of nodes must be fixed and cannot vary. Otherwise, a system is needed that is able to rebalance keys between nodes when nodes are added or removed, and currently only Redis Cluster is able to do this - Redis Cluster is generally available and production-ready as of April 1st, 2015.

参考

遵循CC协议，转载请标注来源