开发常见的Hash函数（二）-Geohash

发表于

intro1：Geohash祛魅
intro2: Geohash原理及常见运算
intro3: Geohash与填充曲线/二进制小数/bitHacks
intro4: Geohash在Lucene/Elasticsearch/Redis等应用

前文介绍数据结构和密码学的哈希函数，本文介绍下带hash的Geohash，即如何把地理空间映射为字符编码。
写作本文的时候，笔者发现一篇比较清晰的Geohash/S2之类的介绍，可以移步高效的多维空间点索引算法 — Geohash 和 Google S2 ，本文会介绍一些前置知识，并结合示例以及其在Lucene/Elasticearch等的应用。

距离计算公式

在了解geohash之前最好先了解通常计算球面距离通常几种方法：
1） 欧氏距离
即两点直线距离，一般是把球面作欧氏平面坐标两点距离，也可以是空间两点距离，后者计算量会多些。两种做法两点经纬度差距太大的话误差也会很大，高纬度地区有cos校正所以误差也会影响。
2）Great-Circle，球面余弦距离公式
即球面的一点A出发到达球面上另一点B，所经过的最短路径的长度，也就是大圆劣弧。运用简单的向量空间即可推导球面三角形的余弦公式：cos(c) = cos(a)cos(b)+sin(a)sin(b)cos(C)，或者也可参考美团的 地理空间距离计算优化这篇文章，推导较简单明了，这里不再贴图表示。
该结果返回的是最精确弧形长，但复杂三角函数导致较慢。
3）Haversine公式，球面半正矢公式
Haversine公式用到的就是半正矢定理，曾经在航海测距上被使用过，wikipedia上给出了从余弦定理推到变换方法，不过中文版描述有误，如 theta和varphi混淆了，而且描述的让人误以为 Haversine 是近似距离
这里是另外一个证明：Deriving the Haversine Formula，
如果你熟悉球面三角学，可以通过球面三角基本式得出结论， 这里是纯粹基于代数向量空间的证明。
这里推荐美团的一篇文章 地理空间距离计算优化。
4）其他
参考这篇文章，Calculate distance, bearing and more between Latitude/Longitude points，笔者用js实现了几种球面距离计算公式，如Haversine可以达到50万/秒次数。
*5）简单补充下：
1） 上述前三种类型，在Lucene和Spatial4j均有实现，分别对应distVincentyRAD、distLawOfCosinesRAD、distHaversineRAD，在Elasticsearch早期可以指定参数选择距离计算使用 arc(Great-Circle) 、plane(平面距离)、sloppy_arc(Haversine距离)其一，不过最新版arc已经替换为Haversine并作为默认实现，且删除了sloppy_arc这个distance type。
redis中使用的是 geohashGetDistance也是Haversine距离距离。
2） 上述 美团文章里，作者还提到了基于Haversine性能优化，以及如何通过曲线拟合消除掉cos函数的，代价是精度降低和开销增加。很值得学习 的一个地方是， 作者使用org.apache.commons.math3.PolynomialCurveFitter，即多项式拟合来拟合cos这个三角函数，消除了cos函数计算 commons.math3本身提供了simple/高斯拟合/多项式拟合，看泰勒级数猜测可能仅3/5次足够。早期cpu fsin之类三角函数指令周期远比乘法大，软件实现由于精度高可能会较为耗时。
不过笔者发现Lucene/Elaticsearch都有计算haversine的优化，sin/cos/arcsin等底层都是用SloppyMath的优化策略，误差在0.01毫米，SloppyMath即是参考fdlibm实现的快速三角函数计算，不过同0.7版本已经直接用java math库了。
spatial4j源于lucene开发，后来独立出来，但代码还是和lucene同步，不过已经几年没更新了，Lucene还在剥离中更新，故下文主要指Lucene。
3）上述计算提到了误差，其实即便Haversine本身计算也是存在误差的，或者说球面余弦计算也会误差，因为地球毕竟不是一个规则的球体，甚至笔者个人觉得距离足够近的话，该结果不如平面距离计算结果精确也可能。所以真实测距可能会借助一些物理手段测量。

Geohash

geohash起源-省市区县作为编码

上面几种方法距离计算其实足够快，如果只是几十万的地理位置进行距离计算，可以看到美团给出的性能数据在毫秒级，感觉搜索附近的人时，直接计算距离也是可以的。
但全量计算毕竟浪费巨大，计算东方明珠附近1km景点没有必要拿全国的景点坐标跑一遍，是否存在一种方案避免呢？
显然存在的，比如最简单的我们可以赋予省市属性，这样可以排除上海之外的其他省市。
上面这种方法真的不如Geohash吗，或许许多都会提及z阶曲线/皮亚诺曲线等空间填充曲线，但笔者认为单是geohash甚至可以无关这些，因为康托理论/z阶曲线/皮亚诺曲线侧重不仅是一一对应更是可数这个关系，不过考虑到大多文章提及，这里先介绍下前置知识，之后再继续上文思路。

康托集合论及康托其人

上文二维映射到一维的数学起源于康托集合论，最简单的例子就是集合的元素个数等于子集的元素个数，比如自然数的数量和偶数(>0)的数量是一样多的，虽然大于零的偶数是自然数的子集，二者可以用y=2*x建立映射关系，更神奇的是有理数的数量和自然数的数量也是一样多，康托提供了一种建立对有理数可数的方式，即自然数和有理数映射关系，这里贴一个经典的图：

按上图用自然数顺序的一直数下去，同时也遍历了所有的有理数。
康托尔提出，提出了基数(cardinal number)，也叫势(cardinality)的概念，来标记无穷集合的“大小”。两个无穷集合之间如果能够建立一个一一对应关系，就说这两个集合有“相同数目的元素”/有相同的势/有相同的基数。
借助康托集合论，我们可以推出许多和常识相悖的令人不可思议的结论：
比如所有的奇数/偶数/自然数/整数/有理数他们的数量一样多即基数相同；
所有的实数和[0,1]区间内的实数有相同的基数；
面的数量等同一条边，比如三角形和它的一条边有相同基数。
数学经历过无理数/微积分/集合论三大危机，在康托/罗素等之后公理化集合系统得以建立，1900年后步入新世纪，基于康托的集合论更是将当时数学一分为三，形成逻辑主义、形式主义和直觉主义三大学派。
笔者认为康托的理论对数学基础的影响不亚于根号2，不说康托集合论是现代数学的基础，但可以说是现代数学正确性的基础，他对无穷的研究不仅是开拓性而且是颠覆性的，现代科学最能与之相比较的就是相对论。
或许是数学理论不如物理理论那样可以通过科学的试验证明，康托没有爱因斯坦那样幸运，早期其理论和个人的观点得到许多批判，不乏顶尖的数学家，如当时法国数学届翘楚/庞加莱猜想的提出者/最有可能比爱因斯坦早提出相对论的庞加莱，以及克莱因瓶提出者克莱因。来自导师的攻击和家庭的不和终导致其一度精神崩溃而入院，恢复后，继续工作，但晚年终在病魔交缠中去世。
希尔伯特/罗素曾评价他是 “是数学天才最优秀的作品”，“是人类纯粹智力活动的最高成就之一”，“是这个时代所能夸耀的最巨大的工作”,”19世纪最伟大的智者之一”。
康托集合论启发了哥德尔的不完备定理，图灵的停机问题，而这些都是现代编程语言的根基。

那么需要Geohash的理由是什么？

接上文，上述地标的方案问题在于需要不存地标信息而且存在边界点问题，所以换种思路，是否可以根据经纬度来呢？
比如画一个正方形，即根据距离和中央点经纬度，我们计算这个正方形的左上角和右下角，即满足条件的点的 经度和纬度的范围(组成一个正方形)，筛选出点之后再计算距离。
这样不需要地标信息，比如在数据库可以通过 WHERE (经度 BETWEEN a AND b) AND (维度 BETWEEN m AND n))筛选即可。
那么有办法通过一种编码快速做到类似功能吗？该功能非常有用，因为早期Lucene/Elasticsearch对于数字尤其是double其实非常不适合做区间查询（下文会介绍下）。

Geohash

看Wikipedia介绍Geohash:
Geohash is a public domain geocode system invented in 2008 by Gustavo Niemeyer and (similar work in 1966) G.M. Morton。
Geohash 2008年为Gustavo发明，但1966年Morton提出了Z-order编码后来以他的名字命名，Geohash即是Morton码的一个现实应用，而莫顿码(Morton code)最初则是为了将二维(或者多维)坐标转换为一维，如两个坐标数的各个位交叉的产生一个新数就是莫顿码，这样的数据不仅适合存储压缩，而且使用一维数据的各种(tree/list)等查找方法。 比如一些删格数据就是用moton码，如地理位置/图像等。
这类编码涉及到空间填充的问题，早在1890年，皮亚诺(Giuseppe Peano)就描述了一种填满一个正方形的曲线的方法，对应曲线叫皮亚诺曲线，Peano curve，这里链接在线看皮亚诺曲线生成。
希尔伯特提出了皮亚诺曲线的变种，希尔伯特曲线，Hilbert curve。Peano变种许多，而后者以简单明了流传，有意思的是Peano特长在发展布尔的符号逻辑系统，奠定现代符号逻辑学。
Z-order 曲线，在Wikipedia上称之为Z-order curve，以此来区分基因分析里的Z curve，中文z阶曲线、z填充曲线等，这篇文章有介绍 Z-Order/皮亚诺/希尔伯特等曲线：高效的多维空间点索引算法 — Geohash 和 Google S2 。
像上述的空间曲线，分形几何相关研究出了许多有趣的结论，如对皮亚诺曲线科赫曲线的研究就有数学家写出“英国的海岸线有多长”的论文，在代数系统里他们属于实分析的分支测度论，比如除了皮亚诺迭代方法可以构造皮亚诺曲线之外，Z-order/希尔伯特等曲线都可找到对应构造方法。
真实的皮亚诺/希尔伯特曲线其实是一套符号系统描述的，非常抽象，但是得益于数学家天才想法，我们还是能通过图形感知这类曲线，这里感受下 Z-order填线：

我们也可以从上文观察到Z-order曲线编码的突变性。
GeoHash vs Z-order curve

GeoHash的运算

二进制小数


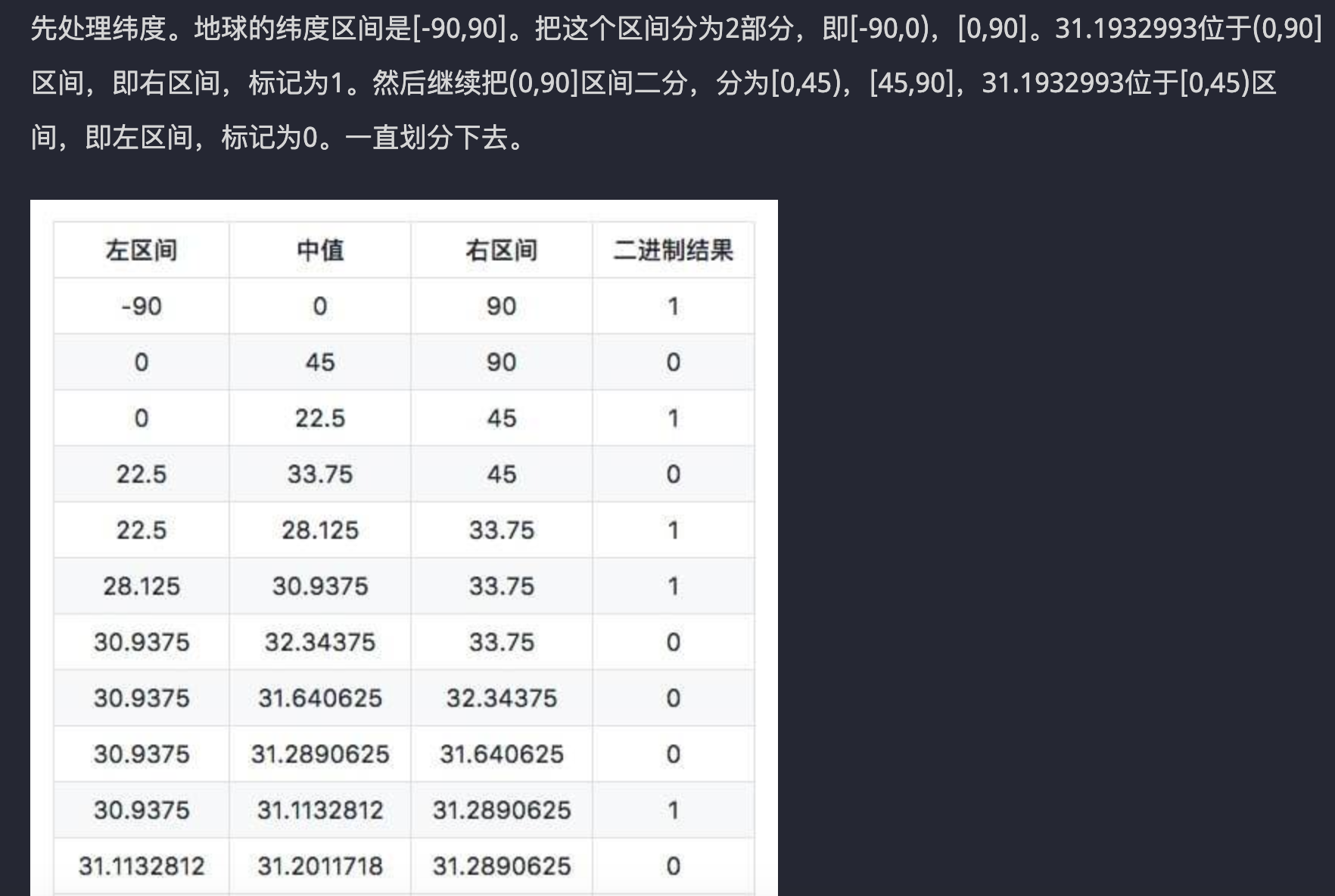大多数文章介绍geohash编码方法时都会用类似上面图举例Geohash如何编码的，实际上Lucene依赖的Spatial4j组件现在却是还是通过一个while循环这么计算的，不过有其他简单的理解，因为这个过程其实就是像一个十进制小数转化为二进制表示，比如 123.41555/180=0.6856419444，而0.6856419444小数二进制表示正是 (0.1010111110000110001110110000001)2，即类似二进制小数编码并移位，因为Z阶曲线或许就采用了康托常用的二进制小数手段。
新版的Lucene的GeoEncodingUtils和Elasticsearch的Geohash就是这个原理去编码的

1
2
3
4
5
6
7
8
public static int encodeLatitude(double latitude) {
  checkLatitude(latitude);
  // the maximum possible value cannot be encoded without overflow
  if (latitude == 90.0D) {
    latitude = Math.nextDown(latitude);
  }
  return (int) Math.floor(latitude / LAT_DECODE);
}

上式中：LAT_DECODE = 1/((0x1L<<32)/180.0D)。
因为long是64位，所以经纬度各分32位，上面式子其实可化为 return (int) Math.floor(Math.pow(2, 31)*(latitude/180.0D))，纬度因为是在 (-90,90) 之间，所以是除以180，经度除以90。
Redis中的geohashEncode也是用这个方法把经纬度编码成32/64位int的。
那么这里你是否也理解了下图中geohash位数带来的误差呢？
Digits and precision in km

geohash length lat bits lng bits lat error lng error km error
1 2 3 ±23 ±23  ±2500
2 5 5  ±2.8  ±5.6  ±630
3 7 8  ±0.70  ±0.70   ±78
4 10 10  ±0.087  ±0.18   ±20
5 12 13  ±0.022  ±0.022    ±2.4
6 15 15  ±0.0027  ±0.0055    ±0.61
7 17 18  ±0.00068  ±0.00068    ±0.076
8 20 20  ±0.000085  ±0.00017    ±0.019

“纬度每相差一度是111.2公里,经度则不同,赤道上经度每相差一度则相距111.2公里,北纬30度则是111.2乘以2分之根号3,北纬45度则是111.2乘以2分之根号2”，geohash长度为1时，纬度占两位，也就是 90/pow(2,2)*111=2500 公里，经度是 也就是 180/pow(2,3)*111=2500 公里，这点和上面度数差类似。
同时我们也可以看到这个图没有说明的是经度差其实并不准确，因为没有考虑高低纬度时各自的1经度距离差是不一样的。
另外，如果你看过上文链接的文章，即Solr空间搜索原理分析与实践，这里提一下，该文章里41.79452,123.41555，对应的geohash是wxrvb2kqexu，这是一个错误，应该是 wxrvb2kqwz0。

Geohash的Base32编码

正如你在wikiedia或文章开头文章看到的Geohash是base32编码的，但是却不能用标准的RFC定义的标准Base32解码，最简单一点是GeoHash 基准字符和顺序是“0123456789bcdefghjkmnpqrstuvwxyz”，去掉了容易混淆的 a/i/l/o四个字符，可以看ES里的编码，而标准base 32 的基准字符和顺序是”ABCDEFGHIJKLMNOPQRSTUVWXYZ234567=”，其中后者的=是填充字符，base32还可以共用base64的码表，标准base32基于RFC 3548/RFC 4648。
所以标准base32 是不能解码geohash的base32的。

Morton编码的技巧

将经纬度化为二进制后怎么进行morton编码呢？正如上文把经纬度转换成两个32位int后如何将他们合并分散到奇偶位上成为一个morton码？
在Redis和Elasticsearch的代码里均可以找到类似代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
private static final long MAGIC[] = {
        0x5555555555555555L, 0x3333333333333333L,
        0x0F0F0F0F0F0F0F0FL, 0x00FF00FF00FF00FFL,
        0x0000FFFF0000FFFFL, 0x00000000FFFFFFFFL,
        0xAAAAAAAAAAAAAAAAL
    };
// shift values for bit interleaving
private static final short SHIFT[] = {1, 2, 4, 8, 16};
public static long interleave(int even, int odd) {
    long v1 = 0x00000000FFFFFFFFL & even;
    long v2 = 0x00000000FFFFFFFFL & odd;
    v1 = (v1 | (v1 << SHIFT[4])) & MAGIC[4];
    v1 = (v1 | (v1 << SHIFT[3])) & MAGIC[3];
    v1 = (v1 | (v1 << SHIFT[2])) & MAGIC[2];
    v1 = (v1 | (v1 << SHIFT[1])) & MAGIC[1];
    v1 = (v1 | (v1 << SHIFT[0])) & MAGIC[0];
    v2 = (v2 | (v2 << SHIFT[4])) & MAGIC[4];
    v2 = (v2 | (v2 << SHIFT[3])) & MAGIC[3];
    v2 = (v2 | (v2 << SHIFT[2])) & MAGIC[2];
    v2 = (v2 | (v2 << SHIFT[1])) & MAGIC[1];
    v2 = (v2 | (v2 << SHIFT[0])) & MAGIC[0];
    return (v2<<1) | v1;
}

这里通过简单的移位且或操作把两个32位的int按奇偶打散成一个64位的long，还是慢神奇的。
这里的hack技巧来自于 Bit Twiddling Hacks 这个神奇的网站，正如题所述关于bit操作技巧大全，从最简单的奇偶判定、n位置1、最右的1置0、1数量等，可以说非常的全了，笔者大学时在读完由微软亚洲研究院的程序员集体创作出的《编程之美》这本书曾惊叹其中的位操作技巧，但看到这个网站还是大开眼界的。

Geohash的neighbor

需要说明的是，Lucene在使用BKDTree之后，这部分功能其实已经没有用了，因为早期采用prefix tree方式，如GeohashprefixTree，而且可能其他系统实现依旧是前缀树，所以这里简介下。
Elasticearch还是可以找到的，geohash模式可能还可以用，代码。
如上文Z-order曲线突变性，以及九宫格解决边界问题，所以需要正确的找到某geohash的邻居，或者说，怎么根据 距离差选择合适的geohash进行搜索？
这里可以看到redis通过经纬度获取周围8个neighbors后再通过矩形经纬度筛选，membersOfAllNeighbors，在该过程后还会再排序。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
int membersOfAllNeighbors(robj *zobj, GeoHashRadius n, double lon, double lat, double radius, geoArray *ga) {
    GeoHashBits neighbors[9];
    unsigned int i, count = 0, last_processed = 0;
    int debugmsg = 0;
    neighbors[0] = n.hash;
    neighbors[1] = n.neighbors.north;
    neighbors[2] = n.neighbors.south;
    neighbors[3] = n.neighbors.east;
    neighbors[4] = n.neighbors.west;
    neighbors[5] = n.neighbors.north_east;
    neighbors[6] = n.neighbors.north_west;
    neighbors[7] = n.neighbors.south_east;
    neighbors[8] = n.neighbors.south_west;
    /* For each neighbor (*and* our own hashbox), get all the matching
     * members and add them to the potential result list. */
    for (i = 0; i < sizeof(neighbors) / sizeof(*neighbors); i++) {
        if (HASHISZERO(neighbors[i])) {
            if (debugmsg) D("neighbors[%d] is zero",i);
            continue;
        }
        /* Debugging info. */
        if (debugmsg) {
            ....
        }
        if (last_processed &&
            neighbors[i].bits == neighbors[last_processed].bits &&
            neighbors[i].step == neighbors[last_processed].step)
        {
            if (debugmsg)
                D("Skipping processing of %d, same as previous\n",i);
            continue;
        }
        count += membersOfGeoHashBox(zobj, neighbors[i], ga, lon, lat, radius);
        last_processed = i;
    }
    return count;
}

ES的获取neighbor方法笔者尚未看，似乎用的是尾递归遍历筛选，但如果利用前文所述二进制应该会简单些，redis就是类似的做法。
同样，也可以看到其实geohash前缀/neighbor方法还是比较粗糙的，比如误差其实还可以考虑乘以cos角，但也可能复杂了，不过上述已经比前文计算全部的距离可以大大缩减了。
像geohashprefixtree就是利用 通常geohash字符串的公共前缀的长度越长，这两个点距离越近（除了突变），反之未必。但其实并不那么适合二维，geohash最好仅用作编码，数据结构可以独立，像lucene提供的quadtree或者bkdtree之类。
所以个人认为，美团技术那几篇文章需要更新了，或者基于solr的实现可以更新了。

Geoash常见系统的实现

上面列出了geohash转换相关知识，那么geohash时怎么被使用呢？

Redis geo

Redis geo提供了几个命令，支持根据位置计算距离，根据某地标或者经纬度计算附近的地标，如详细参考georadius。
使用redis的问题显而易见，一个完全的单热点，地理坐标信息全部放在一个zset 集合中，而且redis又是单线程，不适合大量的地标数据和大量访问。
所以通常不推荐redis做地理位置geohash查询的原因，但是如果你的数十几万以内完全可以使用，不过作为选择也可以试试下面的Mysql方案。

Mysql

最简单的是在mysql中用经纬度直接计算出球面/平面距离作为一列并排序，这个计算可以复杂如三角函数/开根号或优化近似，但大量计算或扫描/加载是不可避免的，量大时性能远不如上文矩形块经纬度作between查询。
不过Mysql有官方实现版本，叫MySQL Spatial Extensions，Mysql的空间扩展，他是一个OpenGIS的实现，可以用来进行实体、空间、位置的计算，对于从事GIS行业的很有用，比如Mysql的geometry定义/geo函数/WKT/WKB值得一看。
其中（如下是基于mysql 5.7之后）：
1）对于两点的距离计算，即两点间的欧氏直线距离(非球面)，Mysql的空间扩展提供了 ST_Length 函数。
2）对于经纬度作between的方法，即矩形包含关系的，Mysql的空间扩展提供了一个MBRContains(g1, g2)函数，用于测试g1和的两个几何的最小边界矩形（MBR）之间的关系g2。
如下，表示loc_point这一列的点数据是否包含在 (lat,lng)这个点附近r公里的矩形内，其中address_point列是SPATIAL/POINT类型，即Geometry，它包含了Point、Curve、LineString、Surface和GeometryCollection几类空间图形，111.12是地球每1纬度的距离是111.12千米，r单位是千米，Polygon即是逆时针点描述的矩形。

1
2
3
4
5
6
7
8
9
10
WHERE MBRContains(
    ST_GeomFromText('Polygon((
        lat-r/(111.12/COS(RADIANS(lng))) lng-r/111.12,
        lat-r/(111.12/COS(RADIANS(lng))) lng+r/111.12,
        lat+r/(111.12/COS(RADIANS(lng))) lng+r/111.12,
        lat+r/(111.12/COS(RADIANS(lng))) lng-r/111.12,
        lat-r/(111.12/COS(RADIANS(lng))) lng-r/111.12  
    ))')
    loc_point
)

函数MBRContains的性能显然比distnce快速，而且和前文的geohash前缀查询可比，因为其使用了R树索引，但显然也受Mysql本身性能限制。
mysql还提供其他丰富的gis/图形位置关系的函数。

Lucene和Elasticsearch里的Geohash

被放弃的PrefixTree

上文大多基于Lucene和Elasticsarch分析geohash，所以这里不再具体展开geohash，不过需要指出的是：Lucene已经计划删除GeohashPrefixTree了
Elasticsarch早期使用的就Lucene提供的PrefixTree（GeohashPrefixTree/QuadPrefixTree），可以通过 tree：geohash/quadtree来指定，但是不仅操作复杂而且容易带来性能问题，
所以prefix tree 6.6就已经全面停止支持了 并预计移除 ，因为后面引入了新的地理图形索引：BKD Tree，其对于LatLonPoint类型索引，经纬度还是按照Z-order编码，只是会转换成一个可比较的8字节数组 intToSortableBytes作为这个document的fieldsData，构造LatLonPointDistanceQuery查询的时候，根据距离计算出一个矩形，即整个过程不再有morton编码了。

prefix tree 存在的问题

在Elasticsearch 2.2之前，geo-point查询是无法直接对应倒排索引的，geo-point本身是作为string或number保存下来，不管是geohashprefixtree还是quadprefixtree，一次典型的geo-point会分为两步(two-phase)，通过geohash前缀或numer范围查询到相关区域(大概像geohash邻居)，然后通过这些区域(token)去倒排索引中再次查询，quad只是比geohash精确些。
Lucene在随着FST后，Block tree逐渐改进，到了Lucene 5.6 KD Tree正式推广，

Lucene早期数字范围搜索问题

Lucene早期对数字类型字段(Numberic)检索时本质上是作为字符，数字被转化为适合排序和适合trie的结构建立索引，范围查询时从trie得可以得到适合前缀的term再进行查询，该方式可以避免补位或者遍历区间所有数的方式查询，但这些float/double转换后的int/long不是没有问题，虽然或许能保持有序但足够大的时候相差为的两个float可能会被转化为相等的int。
数字类型直到Lucene 6.0的BKD tree(elasticsarch似乎5.x即2.4后)才得到进一步优化，大幅性能提升。

Lucene改进 FST vs BKD-tree

trie树可以实现前缀树和后缀树，前缀树较常见，常用与分词和字符串查询，像Lucene中DoubleArrayXX的也是，像Lucene实现的FST（Finite State Transducer）理论上像是一种前缀trie（官方自称burst trie），
这或许也是为什么FST不能直接查询子串(不含分词)或通配符不能用于第一个，子串查询需要使用通配符或正则式模式查询。
但FST类似FSM（FSA/FSM有穷状态自动机，其他如DFA/NFA）， 作者自述其实是基于Weighted Finite-State Transducer，比较深奥，我们比较常见的实现状态机使用的是trie图，如国内某款分词器在用的大名鼎鼎的AC自动机算法（用于字符多模式匹配的）即是trie的实现（基于trie图进行KMP匹配），这种trie图对树前缀或后缀压缩，可以较少的内存保留较多的字典信息同时，查询次数可以保持在O(1)即字符串长度。

所以FST具备速度快/压缩了空间，FST使得加载到内存完全可以没有索引的词，尤其是英文，所以4.0开始，FST成为重要的数据结构，影响后续功能的实现，如正排文件存储部分改动面向FST，(BlockTreeTerms类实现)加入了FST的信息和格式，term聚合到block不再是随即而是按前缀聚合…所以阅读源码最好在4.x之后，比如最主要的Term Dictionary的tim/tix/tip等文件。
但如果你看到 ”xx版本后倒排索引实现为FST tree“或者“xx开始大量使用的数据结构是FST”，笔者认为是较模棱两可的。倒排索引是Lucene的核心之一(basic data structure)，是一种设计思想，Lucene后来引入了BKD tree新的方式进行geo_shape查询，在此之前倒排索引是唯一，的skip list也算一种算法/数据结构，早期Lucene可能用了DefaultSkipListWriter的实现，4.0之后抛弃该类并加入FST同时后续版本也逐渐设计/改进新的skiplist实现，像各个版本产生了各种postings的(writer/reader)，我们常看到Lucene40/50/60/80之类版本好命名的包/writer类/reader类，一般对应索引读写格式的变化，但都存在扩展MultiLevelSkipListWriter/Reader这个存在很久的抽象类的类。
比如7.4版本Lucene50PostingsFormat的BlockTreeTermsWriter在写词典/词索引(Terms Dictionary/index)到tim/tip文件时，就用到了Lucene50PostingsWriter，其内部即是Lucene50SkipWriter，即MultiLevelSkipListWriter 负责根据block的信息写入skiplist，BlockTreeTermsWriter本身会写 .tim(Term Dictionary)和.tip(Term Index)文件，后者用来构建FST，前者用来将FST和postings倒排信息关联，FST拿到的 BlockTermState 信息通过reader的postings定位document，当Disjunction的时候BlockDocsEnum的skip就可能是Lucene50SkipReader实现(doc/pos/payload)，也可以看到其他不同的skiplist实现或相关基于skiplist提供功能的，如ParallelPostingsArray，lucene近20年历史，个人觉得看起来可能会比较跳跃。
elasticsearch的suggest就是基于Lucene的suggest(基于FST)，只不过elasticsearch不是在查询而是在建立索引时就基于segment建立。
不过虽然是一个FSA，FST应该还不能用来实现RegexQuery/Fuzzyquery查询，一个简单的例子是“.*abc+”这样的regex查询，不过Lucene正则查询的确使用到了FST，其添加了自动机（Automaton，FSA/DFA）相关实现，blocktree匹配的时候会分SegmentTermsEnum、IntersectTermsEnum等，后者用于fuzzy/regex查找，AutomatonTermsEnum用于遍历，虽然如IntersectTermsEnum代码所示，正则查询也是依赖FST实现，而且据说速度提高百倍Lucene’s FuzzyQuery is 100 times faster in 4.0。
另外，Lucene的term index，term dictionary等大多数都是pos/docid/skip这种int/long类型数据建立关联，这也是为什么lucene比较青睐对int/long进行压缩。

其他：

1）elasticsearch支持基于 geo_point/geo_shape 的查询，官方文档好懂，DSL使用起来非常容易。
其地理操作目前支持gis主要常见图形和操作，如geo_bounding_box、geo_distance、geo_distance_range、geo_polygon，但语法似乎和geojson有点差别。
2）对于geo_point/geo_shape，提醒一个注意点，Lucene/Elasticsearch接受point定义的多边形时，要求point不交叉，否则构成图形会有问题，这一点要注意。除此外，Lucene似乎未定义多边形点的输入顺序，像其他系统可能要求point的输入必须是逆时针顺序，笔者之前不明白原因，现在想到了，因为在球面上点围成的图形其实是两个，内和外，所以建议最好也逆时针输入。

计划继续写Google S2和Uber以及Lucene的BKDtree，限于时间仅写到这，不过推荐一篇Google S2 是如何解决空间覆盖最优解问题的。
最后，推荐网站在线看全球geohash编码的，因某地图需要翻墙，这里最后贴个图看下世界和中国的geohash效果：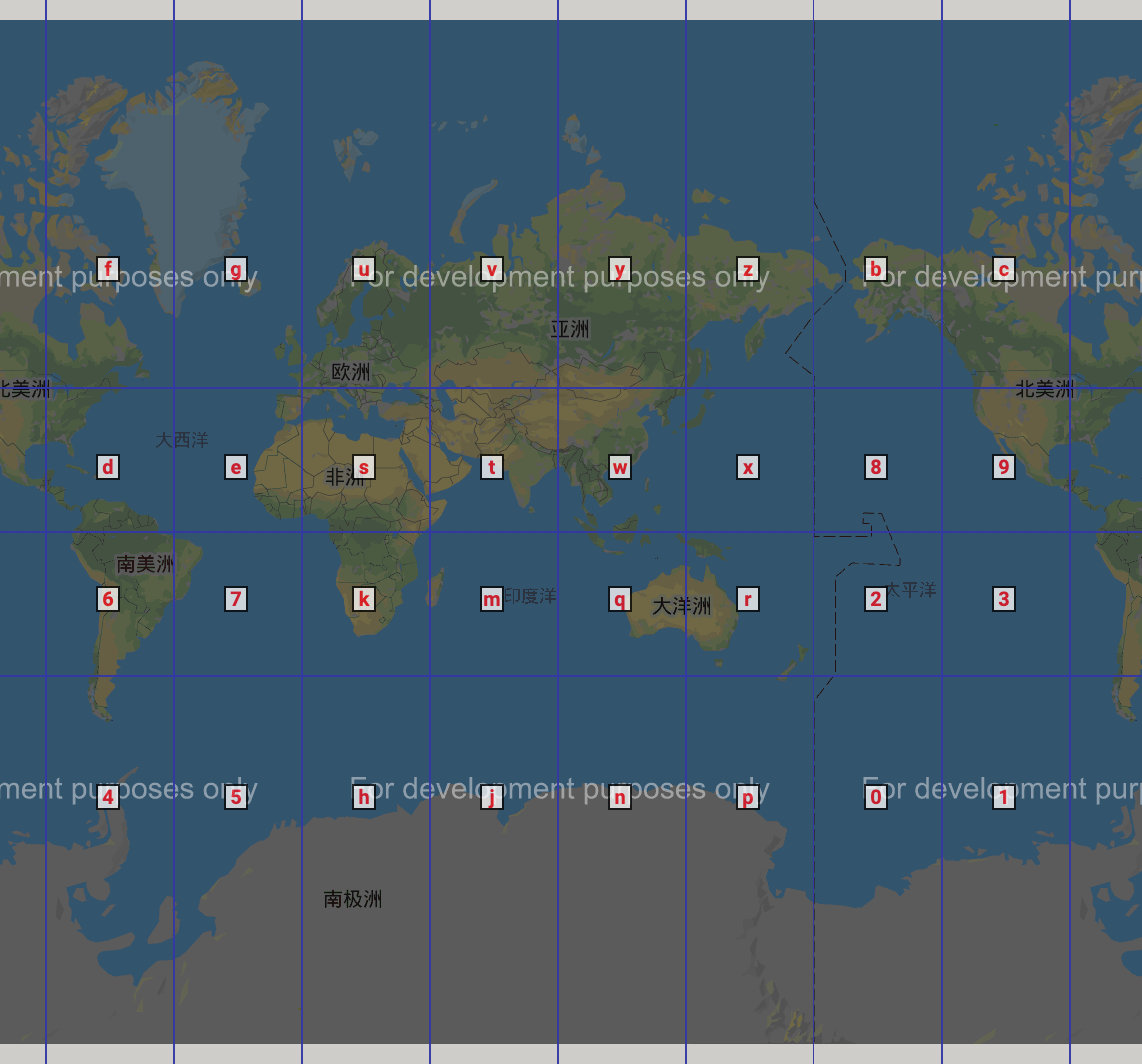


遵循CC协议，转载请标注来源