开发常见的Hash函数(三)-Minhash_Simhash

发表于

intro1：文本相似相关的hash方法
intro2: LSH、Minhash、Simhash
intro3: 基于代码理解minhash/simhash

记录笔者的一些思考，在理解minhash、python minhash源码过程中有不理解或有些搜索不到的，或许在这里得到更多的理解。
前面文章介绍了常规hash，谈到了抗碰撞/雪崩效应等特性，比如微小的改动能产生不同的hash结果。
不过有时候我们期望hash不那么敏感，可以忽略细微的不同，比如一段文字中忽略某些句子顺序，或者忽略几个词的不同，那么有哪些可用的hash方法呢？

需要强调的是，这类hash重点是不敏感，但前提还是期望明显不同的文本hash结果是不一样的，否则我们使用一个常数hash可以做到结果不敏感。即我们期望Hash结果的相似性也最好能代表了文本的相似性，这样可以用来比如判断两篇文章是否相似等。
考虑这类文本hash时，最直接的会想到去考虑对文本特征进行hash，文本最大的特征就是文本使用的“词汇集”，能否对这些词汇做hash达到目的呢？以及图片也是否存在这类hash呢？

匹配场景

我们先看两个例子：
短文本匹配
笔者在某旅游OTA 时曾见过 短文本相似建立关系 的分享，其最初的版本曾使用编辑距离比较，很有效果，但是这种做法也会误判，比如“上海浦东四季酒店”计算“浦东四季酒店”和“上海浦东全季酒店”，后者编辑距离更小，但不是一类酒店，前者才是一类。怎么去避免该类问题呢？
图片相似
在做某学习系统PDF/图片上传功能，笔者曾接到需求要排重PDF和图片避免重复处理。PDF和图片用MD5可以解决部分，但对于微小改动的PDF/图片怎么处理？解析PDF后的文档标题/内容可以去重PDF，但是图片如何处理，尤其是那时开源界尚未有tf，OCR/NLP并不火。
为了下文描述方便，这里简单介绍下海明距离/LSH等，如已知，请忽略。

先了解下什么是 海明距离（Hamming distance）：

wikipedia：
In information theory, the Hamming distance between two strings of equal length is the number of positions at which the corresponding symbols are different.
广义的海明距离定义为两个向量中不同分量的个数，具体数学性质如满足三角不等式等，但在信息论/编码理论中，两个等长字符串之间的汉明距离（Hamming distance）是两个字符串对应位置的不同字符的个数。换句话说，它就是将一个字符串变换成另外一个字符串所需要替换的字符个数。
注意这里比较的是等长字符串，比较不同长度字符串否属于编辑距离的范畴，后者目前常见分为：Levenshtein距离、Hamming距离、LCS（最长公共子序列）、Jaro距离等，维基百科介绍分类比较清晰，如果你看百度百科介绍会比较混乱，不能区分海明距离和莱文斯坦距离。
其中Levenshtein距离在处理字符串比较常见，他是 两个字串之间，由一个转成另一个所需的最少编辑操作次数，允许的编辑操作包括：替换、插入、删除单个字符。计算字符串的Levenshtein距离通常用动态规划算法，Levenshtein自动机可用于高效比较两个字符串限定距离内转化，也就是前一篇文章提到Lucene使用，Levenshtein_distance 这里列出了计算方法以及几种编辑距离不同点。

对于Java来说 Apache Commons Text 提供了：CosineDistance、HammingDistance、JaccardDistance、JaroWinklerDistance、LevenshteinDetailedDistance、LevenshteinDistance、LongestCommonSubsequence-Distance 这些方法比较文本。
numpy也内置了hamming、Levenshtein算法，这里不再详述。
重点看下hamming距离计算方式，对于字符串而言，因为是等长，我们都可以用 if str1[i] != str2[i] dist_cnt++; 来计算，但这里看下对于两个整型数据计算hamming的高效算法，下面是wikipedia上

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
int hamming_distance(unsigned x, unsigned y){
    int dist = 0;
    // Count the number of bits set
    for (unsigned val = x ^ y; val > 0; val = val >> 1){
        // If A bit is set, so increment the count
        if (val & 1)
            dist++;
        // Clear (delete) val's lowest-order bit
    }
    // Return the number of differing bits
    return dist;
}
// Hamming distance for 64-bit integers
int hamming_distance64(unsigned long long x, unsigned long long y)
{
    return __builtin_popcountll(x ^ y);
}

判断不同位的个数，其实可以对两个数进行异或操作并计算这个结果里1的个数，所以上述两个方法都有 x ^ y，只不过1比较常见，通过循环右移并判断末尾奇偶，方法2则是利用内置cpu指令计算快速计算1的个数。
对于64位，计算1个数上述方法1需要循环右移64次，下面改进可以保证循环次数为1的个数

1
2
3
4
5
n = x ^ y;
while (n) {
  count++ ;
  n &= (n - 1) ;
}

这也是python版simhash使用的计1个数方法。simhash直接用来短句比较不是最优的，但是可以学习下他的思路。

先看 LSH 的定义

wikipedia即Locality-sensitive hashing，下面的总结很经典了：

In computer science, locality-sensitive hashing (LSH) is an algorithmic technique that hashes similar input items into the same “buckets” with high probability(The number of buckets are much smaller than the universe of possible input items.) Since similar items end up in the same buckets, this technique can be used for data clustering and nearest neighbor search. It differs from conventional hashing techniques in that hash collisions are maximized, not minimized. Alternatively, the technique can be seen as a way to reduce the dimensionality of high-dimensional data; high-dimensional input items can be reduced to low-dimensional versions while preserving relative distances between items.

不知道你是否发现，前文的Geohash和这里描述的LSH作用很像，接近一种空间上的聚类。
事实Geohash和下文讲的Simhash都是LSH的一类应用，LSH通常用于最邻近搜索（Nearest Neighbor Search, NNS)，即TAOCP称之最近邮局问题(post-office problem)，LSH在编码、压缩、模式识别、基因测序、相似网页等都有应用。
NNS解决方案有
1）精确计算
如线性查询、空间划分，后者包括R家族树以及BSP Tree系列的KD树等。
2）近似计算
贪心算法、LSH（Locality sensitive hashing）、最小内聚。

NNS问题也有诸多变种，比较常见的是K近邻（KNN，k-nearest neighbors）和 近似最邻近查找（Approximate nearest neighbor）等，LSH（Locality sensitive hashing)即本文要讲的就是一种Approximate nearest neighbor查找算法，而且是一种高效的解决方案。

ANN近邻查找/海量网页去重 - minhash/Simhash

LSH用于在高维(high-dimension properties)空间寻找相似性，那么这里为什么会和高维有关系呢？在wordvec中有词向量的概念，比如一个0-1数组(的向量)来表示一个词，向量的长度为辞典的大小，1的位置对应其在辞典中的位置，其他全部是0，但此方法有个维度灾难难于运算，另一种是经过某种训练把词映射为一个短向量，维度很少，一般远少于1000，这些向量构成一个词向量空间，向量余弦距离可以表示相似度，以及像文本预处理也会有特征空间高维性这些概念，LSH就可以用于相似的向量分类达到降维的目的。
Minhash/Simhash过程就包含一种降维手段，将能够表示文本的特征向量映射成低维的特征向量，即一段0-1组成的hash值，两篇文档的minhash/simHash值的Jaccard/海明距离可以代表他们的相似度。
Simhash并非是由Google提出的，只是较早实现并通过一篇论文而被熟知，最初用于从海量的互联网网页中寻找相似的网页，也可用于相似文本排重。举个例子，比如我们怎么判断两篇文章是否一样呢？如上文所述，普通MD5哈希过于敏感，如果希望能够甄别出非标点符号不同以及部分较小改动呢？逐句比较编辑距离是一种方法但未免耗时而且非关键字也能影响结果，分词并统计各自词数也是一种方案，或者早期论文排重里的对比每个段落字数等也是方案。

文本相似度之近邻搜索

在Simhash之前先介绍下同样用于ANN（近邻搜索）的非LSH的几种做法。
下面部分参考自Jeffery Ullman的《Minning of Massive Dataset》（下简称MMD）。
如何比较两篇文章的相似度，或者一般推荐系统中比较两个相似用户？
协同过滤：向量空间模型(Vector Space Model，VSM)似一种最为常见的相似度计算模型，所以最容易想到该方法，可以分为欧氏距离、余弦相似度或者Jaccard也可以用来对此进行相似度等计算（狭义的Jaccard相似度是指两个集合的交集除以两个集合并集）。
比如用户电影喜好问题，可以对每个用户对电影进行0-1打分表示喜好与否，这样通过余弦距离或者Jaccard相似度判断用户是否相似。
k-shigle：文本都可以表示为k-shingles的集合，即每k长字符分割文本得到一系列 k-shingle集，然后比较Jaccard相似度。通常英文选择5到9-shingle集合，Ullman的书有一小节提到如何选择合适的single大小，一般来讲，shingle越长越好，长句通常比短句更有代表性更有区分性，百度的指纹算法也是利用该特性优先使用长句。
编辑距离：即根据文本编辑距离计算，衡量的是文本文字上的距离。

对于文本计算来说，MMD认为k-shingle计算Jaccard相似度的会产生大量的数据，比如对于 4-shingle，数据量可达四倍原文本。而且shingle简单的划分字符串可能很容易因增减助词带来干扰，且任意切割可能使得无法词义上表示文本特征。
协同过滤则因为词库通常比较大，会有高维问题。
此外对于海量文本，上述都需要大量的运算，不过有许多分布式计算如常见mapreduce，而且可对稀疏矩阵计算做优化。另外一种比较有效方法是能否对每个文本构造一个指纹，这个指纹相似度一定程度的代表文本相似度呢？LSH方法即是这种思路，用于文本的常见的有 Minhash 和 Simhash。
不过需要指出，编辑距离不适合长文本，minhash/simhash不适合极短文本(如推特微博等)，文本相似不限于上述几类，比如基于simhash支持权重的S3H准确度高效，基于TF-IDFM模型或LSA/LDA模型/word2vec等支持语义相似度的计算，不是本文重点，故笔者望而止步。
下文探讨两种文本基于指纹去重的，即把一个高维的表示文本的特征向量映射成一个固定bit的指纹(finger print)，指纹的相似度代表了文本相似度：

Minhash

Minhah在最老牌的搜索引擎AltaVista中用于在搜索结果中检测重复Web页。从wikipedia可知Google news还使用其进行新闻个性化定制：
In 2007 Google reported using Simhash for duplicate detection for web crawling[20] and using Minhash and LSH for Google News personalization
minhash正是由在AltaVista工作过的Google杰出科学家Andrei Broder提出（真是需求推动科学理论），MMD书中有对Minhash具体描述，或参考本文 大规模数据的相似度计算：LSH算法，或者minHash(最小哈希)和LSH(局部敏感哈希)，都是以MMD原文解读。
Locality Sensitive Hashing 这篇文章图文结合理解起来清晰。
需要说明的是，最小哈希(minhashing)特指对输入特征集合(这里是一维数组)采用最小哈希算法生成一段指纹，可用于比较两份输入（两个特征集合或特征集合矩阵）之间的Jaccard距离，而通常我们说的属于LSH的最小哈希（Minhash）应该是广义的包括minhashing生成指纹以及通过LSH对生成的指纹矩阵进行hash以便快速找出近似指纹（即近似文本）。
这里借用前一个链接里的图看下 Minhash 包括哪些：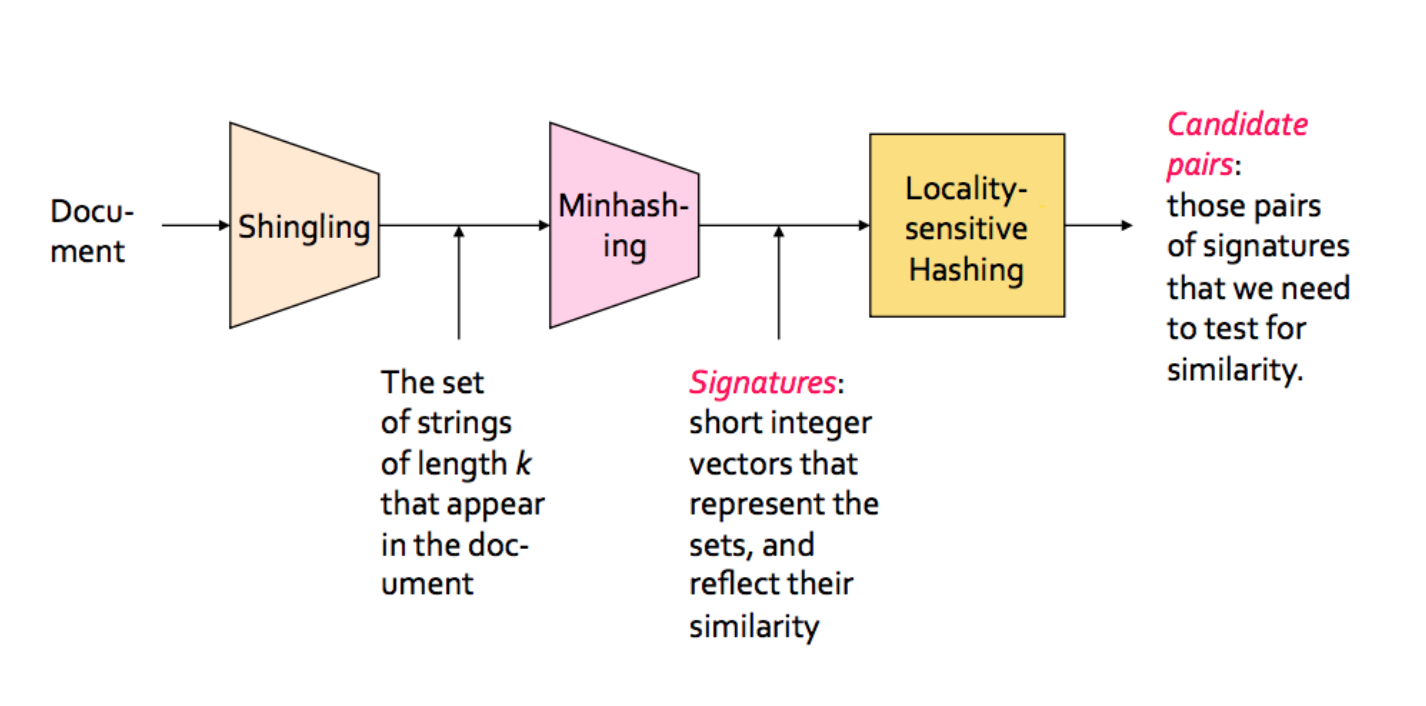

实际上我们看python的MinHash实现，它的输入是一个特征矩阵（下文代码可见），即文档任何可作为特征描述的信息，只不过默认可是shingling，而min hash的查找则是MinHash LSH的几个类实现的。
spark的minhash输入也是一个输入矩阵（一个稀疏矩阵的压缩表示），只不过把minhashing和minhash LSH放到同一个scala类里实现。

minhashing

这里不详述minhashing算法(上述链接已有)，只是做些补充或讨论便于理解。
minhashing有多种变种实现，常见有多哈希函数和单一哈希函数版本。MMD描述的就是多哈希实现。不过笔者认为原文介绍minhash时组织的不够清晰，大部分应该会觉得比较两个文档Jaccard集为什么不直接求交集(也只需遍历特征集一遍)而要用多次交换矩阵每行并求首位1的方式？
首先存储特征向量耗费大量空间，不如生成指纹占用空间小，这点很重要，因为生成最终指纹才是本算法的目的。而且这么做也是为了查找时不需要再做大量求jaccard计算，如果指纹相似那么可以设计一种算法快速查找。生成指纹对应minhashing过程，便于查找对应minhash LSH过程。
1）minhashing的输入是特征矩阵中的一列，即对应一个文本的特征集合，该集合是文档在特征矩阵所有元素关系的一个0-1表示，即如果集合中包含该元素，则矩阵中的该列对应位置为1，否则为0。
但为了理解可把特征矩阵作为整体来看，计算最小哈希的时候就是先把矩阵随机选择两行进行交换，把打乱后的每列第一个值为1的行所在的行号作为本轮计算该列的最小哈希值。
2）在MMD中，作者论证了经行打乱后的两个集合计算得到的最小哈希值相等的概率等于这两个集合的Jaccard相似度。
作者首先说明 SIM(S1,S2) = x / (x+y)，这是容易理解的，因这就是Jaccard相似度的定义，因为Z类表示两个聚合均无，所以就是 x / (x+y)，但是怎么理解 “经过行打乱之后，对特征矩阵从上往下扫描，在碰到Y类行之前碰到X类行的概率是x/(x+y)”呢？首先假设在S1扫描到1时，因为Z类要求二者均为0，那么S2只能是X或Y类，所以是1的概率就是 x / (x+y)，即h(S1)=h(S2)的概率等于 SIM(S1,S2) ，显然前提是二者为独立事件且S1、S2相似的假设。这也是为什么 minhash只能做否定的判断(存在false positive可能性)。
另外上述只是单次随机采样，要做到无偏差估计需要多次采样即重复上述过程。
3）上述随机交换矩阵行高维矩阵时是非常浪费的，是否存在不交换行计算的签名矩阵的方式？ MMD在3.3.5章节最小哈希签名计算 提供了方法，或者上述链接可看到图示该过程，不详述，这里补充下：
1）图示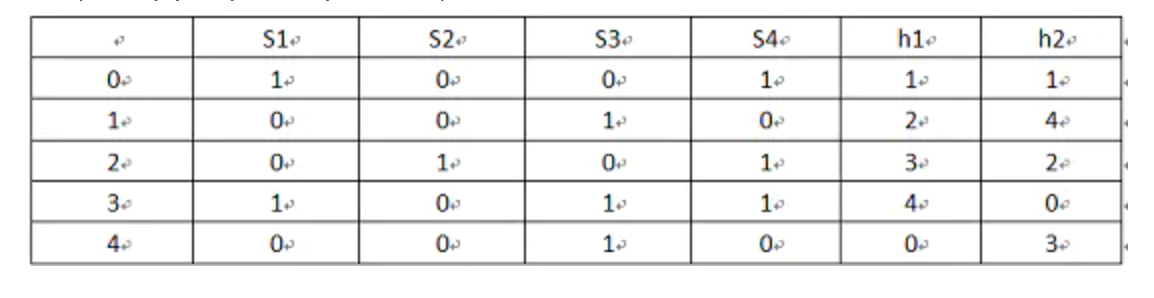

这里是容易看不明白的地方，其实图示第一列是原文档的顺序（暂理解为原始矩阵行id），h1/h2 两列都是第一列的乱序排列，即是第一列的shuffle或者python/spark minhash 里的置换（permutations）概念，h1列的1表示原来行id为0的置换到矩阵第1行。
或许换成下图容易理解些（该图在前一个链接可见），不过下标从1开始。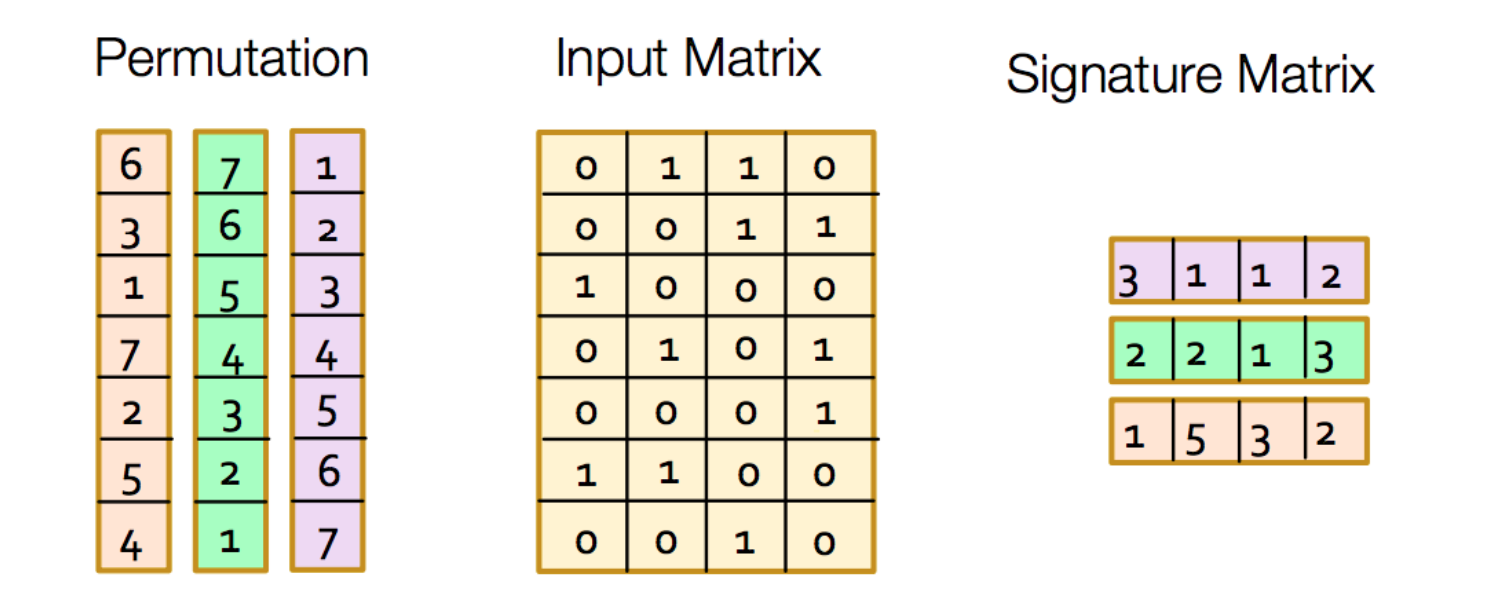

左边相当于置换即h1/h2/h3，中间是S1/S2…，右边是本轮指纹，注意颜色对应。
2）为什么这种做法就等价MMD里描述的行置换方式，即“每列第一个值为1的行所在的行号作为本轮计算该列的最小哈希值”？
MMD原文有些跳跃，可能许多文章没提到，如果我们只看一列，即只用h1列演示一遍就能发现这种更新hn矩阵的做法和原矩阵置换找到最先为1的行号是一样的，只不过从上往下扫描的做法是按照从小到大找到第一个为1截止更新行号，而该做法是遍历所有行号找到对应为1的最小行号。
这里虽然平均多了一倍遍历，但是避免了行置换。
3）更多特性：特征顺序不影响minhashing结果
这个特性是为了下面讲述python/spark实现minhashing算法准备的，大部分文章没有提及，所以笔者在看minhash的python实现时觉得有点困惑，希望这里的分析有助你更好理解python/spark实现原理。
上图中特征集$S1(10010)$，可以看成$S11(10000)$与$S12(00010)$的合集，如果我们分别对S11和S12分别进行h1/h2运算会得到什么结果？
已计算得到: $(h1(S1), h2(S1))=(1,0)$
计算$(h1(S11),h1(S12))=(1,4)$，$(h2(S11),h2(S12))=(1,0)$，继续对$(1,4)$和$(1,0)$ 按列求最小值合并得到：$(1,0)$，同时S11和S12交换顺序再合并不影响$(1,0)$结果，这个结果和$(h1(S1), h2(S1))=(1,0)$一致。
即$(min(h1(S11),h2(S11)),min(h1(S12),h2(S12))=(h1(S1), h2(S1))$。
这里的道理其实和mmd里的最小哈希签名计算道理同，只是多了一次min理解。
这也是为什么特征向量对minhashing来说是看成特征集，即特征的顺序不影响minhashing的结果。

python/spark中的minhashing

这里使用datascketch里的minhash，该链接完整代码，这里列出部分。

1
2
3
4
5
6
7
8
9
10
11
12
from datasketch import MinHash
import random
data1 = ['minhash', 'probabilistic', 'data', 'structure']
data2 = ['minhash', 'probability', 'data', 'structure']
random.shuffle(data2)
m1, m2 = MinHash(), MinHash()
for d in data1:
    m1.update(d.encode('utf8'))
for d in data2:
    m2.update(d.encode('utf8'))
print("Estimated Jaccard for data1 and data2 is", m1.jaccard(m2))

上面是使用方式，同时笔者加了shuffle是为了展示输入/特征顺序不影响结果。
可以看到 datasketch 的核心 MinHash代码即是update方法，即如下一段

1
2
3
4
5
6
7
def update(self, d):
    hv = self.hashfunc(d)
    a, b = self.permutations
    # print("a %s ,b %s ,hv %s" %(a, b, hv))
    phv = np.bitwise_and((a * hv + b) % _mersenne_prime, np.uint64(_max_hash))
    self.hashvalues = np.minimum(phv, self.hashvalues)
    # print("phv %s self.hashvalues %s " % (phv,self.hashvalues))

首先说明下，datasketch MinHash默认使用128个32-bit整数保存指纹，上述链接官方列出测试128次置换时精确度和性能俱佳。其次,原代码是输入参数是b，为免于混淆笔者这里改为d。
上述代码中 _mersenne_prime是一个梅森质数，为$(1 << 61) - 1$，用于实现随机置换效果，_max_hash是$(1 << 32) - 1$，为了控制phv结果32位，hashfunc默认sha1_hash32，为了效果随机。
a和b都是一个由128个64位伪随机产生的整数组成的数组（其中a中数皆大于0），因为seed默认是1，所以所有的Minhash产生的a和b是一样的，a/b被用来产生新的随机数实现置换行。
这里解释下原理，
1）每当特征集的一个特征通过update加入时，hashfunc对其hash得到32位int，也就是说 datasketch 默认把所有的特征映射到 32位int 的空间里，也就是一个 $(1 << 32) - 1$ 维度的向量，还记得上文分析把特征集S1分拆成特征S11和S12运算结果相同吗，这里就是利用这个原理。
2）怎么对 特征 进行运算呢？即例子中的$h1(S11)、h2(S11)$运算？
上述代码里设计 phv 的两行即是，核心的理解就是在这里了：

1
(a * hv + b) % _mersenne_prime

是为了产生随机数，而 np.bitwise_and 保证运算结果在0-_max_hash之间，需要注意的是a、hv、b都是数组，所以这里的 phv 也是一个128长度的整数组，我们知道输入d是单个的特征向量，及其类似S11，只有一位是1，其他都是0，所以 phv 即是待置换的行的index，也就是说本轮对其置换后求最小位就是 phv（注意phv是128个置换函数产生的128个(不同)结果），即这里就是模拟置换操作，再次执行 $np.minimum(phv, self.hashvalues)$ 就是最终minhash结果了。
spark同样也是利用上述原理，其核心代码如下，不再详述：

1
2
3
4
5
6
7
8
9
10
11
@Since("2.1.0")
override protected[ml] def hashFunction(elems: Vector): Array[Vector] = {
    require(elems.nonZeroIterator.nonEmpty, "Must have at least 1 non zero entry.")
    val hashValues = randCoefficients.map { case (a, b) =>
      elems.nonZeroIterator.map { case (i, _) =>
        ((1L + i) * a + b) % MinHashLSH.HASH_PRIME
      }.min.toDouble
    }
    // TODO: Output vectors of dimension numHashFunctions in SPARK-18450
    hashValues.map(Vectors.dense(_))
}

MinHash LSH

上述minhash只是将文档转换为一个指纹，但如何在海量的minhash结果中通过Jaccard相似找到匹配的指纹？毕竟不可能遍历全部指纹去比对，即是否有办法对指纹建立索引呢？
这就是MinHash LSH要解决的问题，由于其比minhash本身易理解，故这里只简单介绍下。默认相似度计算是Jaccard相似度，也就是说比如默认选择128次函数运算（置换）得到最终128个元素组成的签名，我们希望找出有最多下标同且值相等的签名，即该如何在海量数据中建立索引满足这种需求？实际上使用B树或跳跃表都能实现这个需求，而使用简单的分段（range）的方法+倒排可能是大多数人想到的，即分桶的方法，MinHash LSH即是使用分桶策略，但是128层桶可能带来太多的比较次数或空间，MinHash LSH提出了一种 band（段）的概念，一种宽范围的桶，其实理解成区间更易懂，即：
每个指纹签名向量被分成了几段（band），如果两个向量的其中一个或多个band相同，那么这两个向量就可能就相似度较高
但这种分桶的方法会带来两种需要考虑的问题：

  • False Positives:
    相似度很低的两个向量被哈希到同一个桶内
  • False Negatives:
    真正足够相似的向量在每一个band上都没有被哈希到同一个桶内

对于前者或许可以通过再次比较排除，但是对于后者怎么处理呢？实际上MinHash LSH算法默认是不要求处理的，即当真相似的向量每一band上都没有被哈希到同一个桶内时，这次查找就失败即不存在匹配相似度的指纹，也即MinHash LSH是一个近似而非精确的查找。
所以MinHash LSH面临的第二个问题是怎么控制 False Negatives（或者False Positives），原论文作者分析了当 band个数为b，每个band内的行数为r，要求指纹相似度是s时，
两个指纹签名向量至少有一个band相同的概率为$P(exist)=1-(1-s^r)^b$。
对应曲线：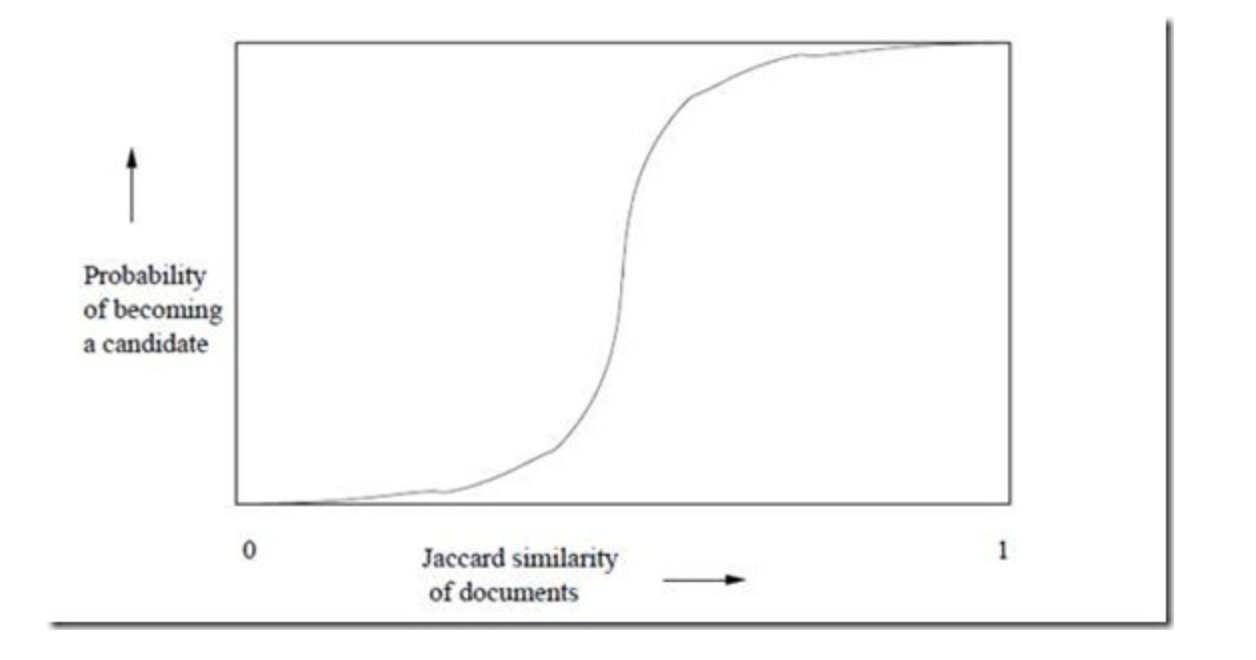

了解到该函数的性质后，我们可以通过计算r,s,b的关系来控制False Positives/False Negatives达到目的。
这个方法是针对Jaccard相似度查找的折中方案，但误判率是存在但可控的。
这里留两个问题：
1）MinHash LSH删除一个元素时需要哪些操作呢？
2）是否可用前一篇文章里的 FST 替代MinHash LSH呢(通过补位和编辑距离)？

其他minhash LSH实现还有：MinHash LSH Forest 支持更少空间和Top-k查询以及MinHash LSH Ensemble修改相似度计算规则，支持基于量而不是Jaccard值，后者要得益于minhash是一个近似count-min sketch，可以估算集合数量。上述可以参考 datasketch MinHash LSH Forest，具体需要进一步探索。这里提供了一个结合Hyperloglog的minhash实现 HyperMinHash: MinHash in LogLog space

Simhash

介绍完minhash，理解simhash就简单了，实际上simhash和minhash有许多类似，Simhash其实也包括simhashing和LSH两部分，即生成指纹签名和指纹查找。只不过simhash指纹生成策略不同，使用海明距离衡量相似度，这也导致其LSH要比Minhash LSH简单些。
Simhash的指纹通常默认是64位的，如python simhash即是，这和上文minhash使用128组32位作为指纹不同。对于64位Simhash的海明距离默认在3以内的都可以认为是相关度高的，这也带来一个优势是在分桶的时候只需要分四个桶就能保证相似的指纹必定会至少一个桶是一样的。
Simhash接受的输入是默认是特征集（虽然它和minhash一样都可以用k-shingle建立特征集作为输入，但通常是Google论文提供的是文本词语的特征输入），下面看下simhash常规流程：
原文档总结很清晰了：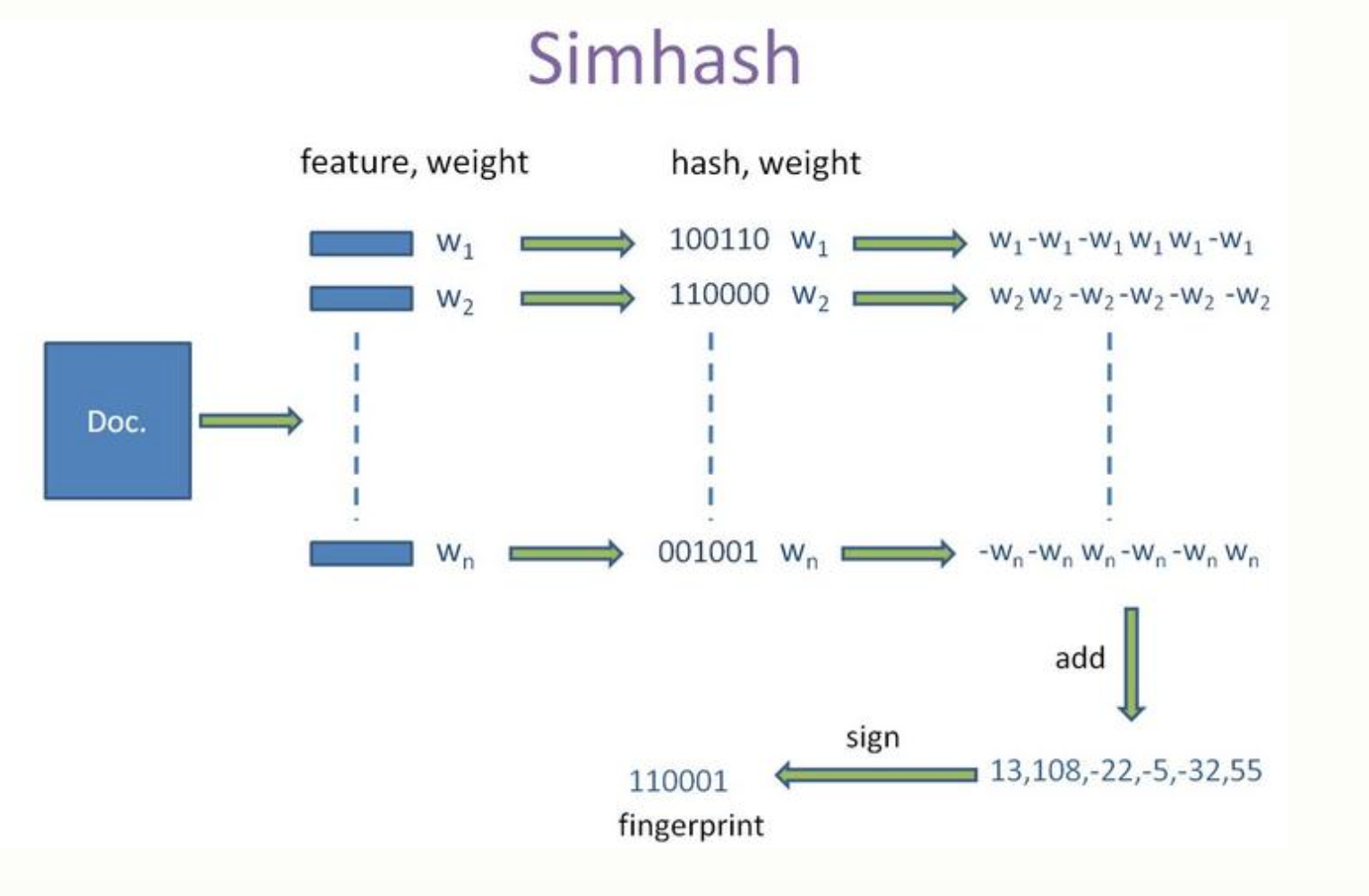

具体步骤：
1，初始化：f维的向量V置0，f 位的二进制数S置0；
2，对每一个特征运算：
1）用hash该特征产生一个f位的签名b。
2）从i=1到f遍历b，计算权重w，默认是1，否则是特征里对应权重。
3）加权：若i位为1，则V的第i个元素加上该特征的权重；否则V的第i个元素减去该特征的权重。
3，更新签名：若V的第i个元素大于0，则S的第i位为1，否则为0；
4，结束，S即为签名。
python simhash实现
先看 python simhash 核心的特征运算部分：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
def build_by_features(self, features):
    v = [0] * self.f
    masks = [1 << i for i in range(self.f)]
    if isinstance(features, dict):
        features = features.items()
    for f in features:
        if isinstance(f, basestring):
            h = self.hashfunc(f.encode('utf-8'))
            w = 1
        else:
            assert isinstance(f, collections.Iterable)
            h = self.hashfunc(f[0].encode('utf-8'))
            w = f[1]
        for i in range(self.f):
            v[i] += w if h & masks[i] else -w
    binary_str = ''.join(['0' if i <= 0 else '1' for i in v[::-1]])
    self.value = int(binary_str, 2)

其中默认是64位结果，hashfunc是对输入进行md5运算并将结果转化为int值，可以看到初始化v，masks，$h & masks[i]$即是用来判断i位是否为1，这里也可以看到如果输入特征集的项不是string的时，必须为collections.Iterable，且第二元素必须为其权重。
比如特征向量为文本分词时，设置的权重时候可以是词频即出现次数，或词的本文权重，也可以是使用的词库设置的权重，甚至也可以自定义。
需要说明的是这里的特征向量集即features参数长度是不受限制的，不要求64个。
python simhash除了上文支持build_by_features之外，默认还支持如下几种构造方式：

1
2
3
4
5
6
7
8
9
if isinstance(value, Simhash):
    self.value = value.value
elif isinstance(value, basestring):
    self.build_by_text(unicode(value))
elif isinstance(value, collections.Iterable):
    self.build_by_features(value)
elif isinstance(value, numbers.Integral):
    self.value = value
else:

其中basestring就是字符串（文本），默认对字符及中文做4-shingle

1
2
def _slide(self, content, width=4):
    return [content[i:i + width] for i in range(max(len(content) - width + 1, 1))]

Simhash含义

笔者并未找到对于Simhash的证明，看论文作者总结部分 FUTURE EXPLORATIONS似乎准确率是未证明的，不过wikipedia上该方法被归类为随机投影(Random projection)一类，随机超平面+余弦距离,$Pr[h(x) = h(y)] = 1 – d(x,y)/\pi$，不过笔者认为这里映射降维时向量之间距离信息变化大小在原文Simhash算法上没有体现出来。
这篇名校的课件比较全的介绍LSH/minHash，推荐。
Simhash的查找，如上文所述，simhash默认64位，默认分成的4块，每一块会建立倒排索引，像python simhash使用hashtable/list等存储倒排，分块遍历。

simhash和minhash对比

Simhash和Minhash都含有LSH的想法，对输入特征信息生成固定长度的指纹，都可以做到对同样两个文档哈希之后保持相似，不同文档哈希后极低概率相似，Simhash采用海明距离计算相似性，而minhash采用Jaccard距离。
另外Simhash指纹通常64位，Minhash不限制，不过许多实现是128组32位整数，Minhash查找算法比Simhash复杂些，且有一定的概率误判。
Simhash还可以实现用户相似度类似的功能，如上文提到的Google news。

“Simhash用于比较大文本而非小文本”，如果这里的小文本并非指的是短语/句子的话，这种说法其实就不太准确，Simhash和Minshash本身只是对特征向量集进行运算，特征向量才是和文本比较精准度更相关的，比如Simhash和Minhash均可支持k-shingle的运算。

在其他文章里有对Simhash和Minhash判断相似性的准确率高低比较，笔者认为回答这个问题前要先清楚如何定义“相似性”，如果相似只是纯粹的文字/内容上的相似（或者说形似），那么Minhash基于k-shingle的做法更能区分形似。如果是针对那些打乱部分文字/句子先后顺序的，洗稿的，甚至不形似但是用词重合度高的使用 Simhash 更合适。
Simhash感觉关注重点在特征的选取上，或许这也是原论文为什么说“Near-Duplicates”。
需要指出的是Simhash/Minhash的结果都是不受单个特征的输入先后顺序影响的。

图片相似计算

前面写的有点多，所以这部分拆出来放在下一篇了。

参考

遵循CC协议，转载请标注来源